注意
这份笔记还处于实验和编写阶段. 可能很多内容会大改, 并且正确性不能够保证, 仅做预览使用.
来源
这份讲义大部分照抄了南京大学魏恒峰老师的离散数学课件和NJU问题求解课程编写组提供的课件和补充资料. 在这里为他们辛苦的准备讲稿以及无私地开源供外校学生学习表达感谢以及敬佩!
查看最新版本
请参看Github的源代码仓库 https://github.com/shzaiz/dx-public/blob/main/TeXify/pypsolve/pypsolve-main.pdf.
问题求解: 第一部分
计算机为什么能够帮助我们这么多? 这一部分我们来简单给出一些答案. 具体地, 我们将会了解计算思维最核心的概念了解计算的基本方法与局限; 同时接受基本的形式化训练掌握抽象数学证明的基本方法.
心智的活动, 除了尽力产生各种简单的认识之外, 主要表现在如下三个方面:
(1) 将若干简单认识组合为一个复杂认识, 由此产生出各种复杂的认识.
(2) 将两个认识放在一起对照, 不管它们如何简单或者复杂, 在这样做时并不将它们合而为一. 由此得到有关它们的相互关系的认识.
(3) 将有关认识与那些在实际中和它们同在的所有其他认识隔离开, 这就是抽象, 所有具有普遍性的认识都是这样得到的.
–John Locke 有关人类理解的随笔, 1960
电脑之所以叫“电脑”, 就是因为它能替代部分人类的思维活动. 回忆每个班上都有一个笔记和草稿纸都工工整整的Ta, 比如布置了一个很繁琐的任务, Ta总是认认真真默默画完. 很显然, 工整的笔记可以启发思维, 但是当问题范围更加大的时候非常困难继续进行.
学过编程的我们如果有良好的计算思维的时候, 就可能有这样的感慨:
烦死了! 劳资不干了! 玩更有趣的东西去了! –一名具有良好计算思维的同学
这就是计算思维: 写个程序 (如model checker) 来代替我们一部分的机械的思维活动. 任何机械的思维活动都可以用计算机替代, Al还可以替代启发式/经验式的决策.
我们在学习英语的时候很重要的一部分是语法(grammar): 也就是什么样的语言是可以被接受(acceptable)的. 比如下面这个英文句子是没有语法错误的:
Fuhai Zhu said that this test is only a small test, so don’t panic.
但是这句话不同人有不同的理解方式, 这就是这句话的语义(schematics).
简而言之(不严谨) , 现在我们有一个由一堆字符串和推导规则组成的形式系统(formal system), 语法决定了这个形式系统能生存什么样的字符串, 而至于这些字符串有什么样的含义则是语义的范畴.
语法类似材料, 语义类似与材料组成的各种建筑物, 我们可以通过语法研究语义层面的推导, 同时也可以从语义层面捕获语法中内涵的结构, 其实语法和语义是相互区别又紧密联系, 即从范畴论的角度看语法和语义是伴随的(其实不同的人做数学证明可以有不同的风格: 偏语法和偏语义, 不过大部分数学家更喜欢语义风格的证明, 可能因为更直观, 更容易被人脑接受. )
𝕋ools
在浏览器中输入 https://pythontutor.com/visualize.html, 你就会得到一个Python代码执行可视化((visualization)的机器. 当对于程序执行的结果感到存在疑问的时候, 我们可以用这个网站观察Python是如何“解释”你的代码的.
比如, 下面这一小段代码:
1for i in range(10): 2 print(i**2)
点击Visualize Execution就可以了, 你可以点击Next来继续模拟执行下一步.
在这里, 你可能会看到很多新奇的名词: 什么是Global Frame, Object? 暂时先不用管. 不过你确实可以看到点击Next的时候Print output一栏一步一步的模拟了你的代码.
通过观察可以发现, 代码按照行数执行, 一次执行一行, 每一次执行计算机内部结构的状态(右侧的面板). 下面我们化繁为简, 来看一看一个系统(数学意义上)能够完成任何人类完成的操作需要的最小可能的操作是什么.
如果我们说, 写出来一个可以计算“我们想要计算的任何理论上能够计算的东西”并不难, 你会不会认为这件事情是无稽之谈? 毕竟计算问题多种多样, 有一些内容涉及到很复杂的判断. 但是, 我们可以用一个很小的指令的集合来描述“我们可以计算的一切事物”. 我们不妨从日常生活中找一点灵感.
𝔼xample:
(等红绿灯) 观察红绿灯, 如果(if)是绿灯, 那就通过这个路口; 否则(else)继续等待. (遵纪守法的好公民)
(做作业) 明确今天的作业范围, 从第一题开始写, 写完题目或者(or)一题目没有思路之后做下一道题, 直到(until)做完所有的问题.
(排序成绩单) 获得班上同学的所有成绩单, 拿一张新的白纸打好表格, 每一次(for each time)从成绩单中选取最大的分数, 把那一行抄写到新的白纸上. 之后把原来那张纸上的内容划去. 一直重复下去, 直到原来的成绩单上没有任何可以被划去的内容.
我们需要找一些东西来具象化我们脑子中的“红绿灯的状态(state)”, “现在在做作业的题目编号”, 这些内容, 因此我们就希望把这些抽象出来. 因此我们有了变量(variable)的概念, 也就是值存在的空间.
把上面的三个内容转化成伪代码(不唯一)就是:
1------ GO THROUGH CONJUNCTION ------ 2if traffic light’s color is green: 3 go pass by 4else 5 wait 6 7------ DO HOMEWORK ------ 8range = [a..b] 9working on problem = a 10while working on problem <= b: 11 finished this problem or can’t work out 12 working on problem = working on problem+1 13 14------ SORT EXAM SCORE ------ 15list = get the source table 16result = empty(for now) 17while list is not empty 18 k= get the max element of list 19 write k to the next line of result 20show result
其实要是能够构造出任何程序的“原材料”(也就是我们的指令集)并不复杂. 无非就是变量(variable)的赋值(assign), 判断(judgement), 跳转(jump), 终止(terminate). 也就是, 如果你能声称有一套系统可以自动化的解决这四个内容, 那么这个系统就具有机械化地做任何人类做的事情. 换句话说, 你可以用这个工具创造整个世界.
𝔻ialogue
A: 创造整个世界? 感觉好中二!
B: 有道理. 但是, 计算机的发明极大地解放了人们的计算能力, 我们只要描述更加聪明的东西, 计算机就会帮我们做更笨重的机械化的指令–而且几乎不会出错!
A: 有点意思, 毕竟我算个两位数乘两位数有时候都能出错...
B: 是的, 不过这个可以交给计算机. 我们就可以专注于研究更加“高等”和“深刻”的内容了.
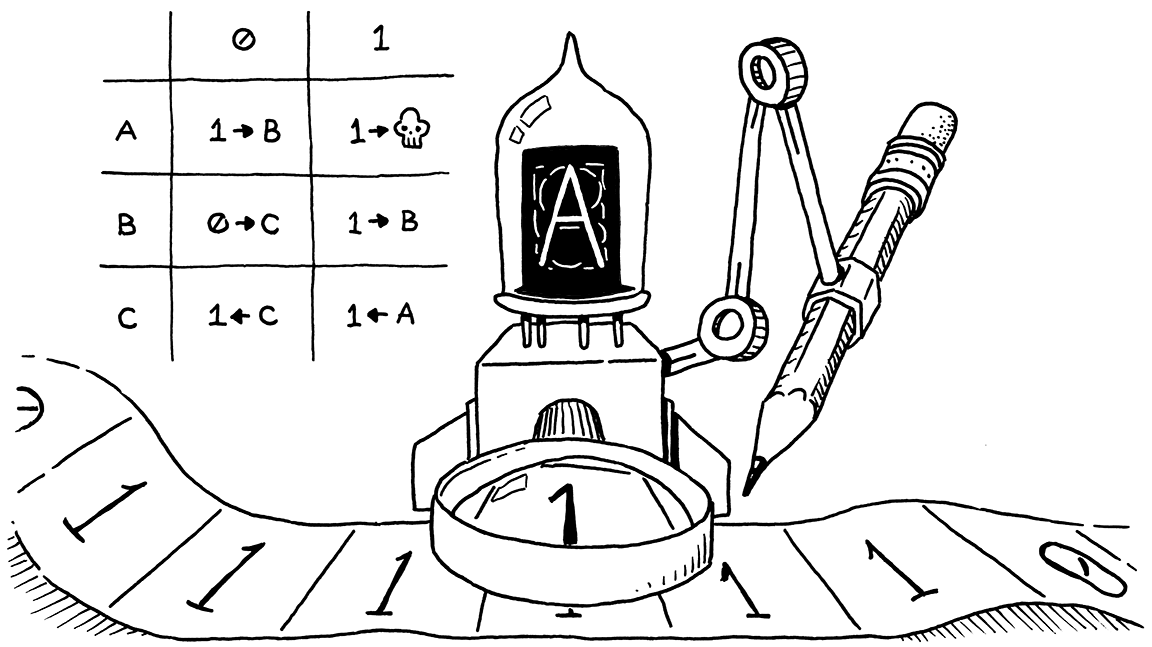
其实用“机械化”的方法代替人力这样的想法是在计算机诞生之前就是人们孜孜以求的问题. Alan Turing 在1936年就提出了这样的设想. 他就是由只一条(无限长)的纸带和一根笔(可以改纸带的内容, 并且查看纸带的内容并据此做判断), 并且有一个程序(墙上的表格), 指示下一步要往哪转移. 只要能够移动读写头, 写纸带的某一个格子, 读纸带的某一个格子, 跳转, 以及终止. 根据计算领域里的证明, 可以得到这个机器就和我们人类的计算能力等价.
这是最早的图灵机的原型.

𝔼xample:
运行图片1.1的程序, 左右按照我们的左右进行(规定ABC右移一格是ABC).
(1) 现在机器的状态是A(头部的字母), 看到的是1(放大镜的字母)
(2) 于是把当前的格子改为1, 纸带向右移动一格, 然后停机.
假设当前纸带的放大镜看到的是0, 再运行一次:
状态:A 纸带状态: 0 1 1 1 0 1 1 0 0
(1)现在机器的状态是A(头部的字母), 看到的是0(放大镜的字母), 执行第一行第一列的指令1(改为1) →(向右移动一格)B(状态改为B) .
状态:B 纸带状态: 0 1 1 1 1 1 1 0 0
(2)现在机器的状态是B(头部的字母), 看到的是1(放大镜的字母), 执行第二行第二列的指令1(改为1) →(向右移动一格)B(状态改为B) .
状态:B 纸带状态: 0 1 1 1 1 1 1 0 0
(3)现在机器的状态是B(头部的字母), 看到的是1(放大镜的字母), 执行第二行第二列的指令1(改为1) →(向右移动一格)B(状态改为B) .
状态:B 纸带状态: 0 1 1 1 1 1 1 0 0
(4)现在机器的状态是B(头部的字母), 看到的是0(放大镜的字母), 执行第二行第一列的指令0(改为0) →(向右移动一格)C(状态改为C) .
状态:C 纸带状态: 0 1 1 1 1 1 1 0 0
(5)现在机器的状态是C(头部的字母), 看到的是0(放大镜的字母), 执行第三行第一列的指令1(改为1) ←(向左移动一格)C(状态改为C) .
状态:C 纸带状态: 0 1 1 1 1 1 1 0 1
(6)现在机器的状态是C(头部的字母), 看到的是0(放大镜的字母), 执行第三行第一列的指令1(改为1) ←(向左移动一格)C(状态改为C) .
状态:C 纸带状态: 0 1 1 1 1 1 1 1 1
(7)现在机器的状态是C(头部的字母), 看到的是1(放大镜的字母), 执行第三行第二列的指令1(改为1) ←(向左移动一格)A(状态改为A) .
状态:A 纸带状态: 0 1 1 1 1 1 1 1 1
(8)现在机器的状态是A(头部的字母), 看到的是1(放大镜的字母), 执行第一行第二列的指令1(改为1) →(向右边移动一格) †(停机)
状态:A 纸带状态: 0 1 1 1 1 1 1 1 1
下面我们来看一看为什么说可以用Python语言的计算能力和他们是等价的. 在这之前, 我们先来了解一下如何获取帮助和得到通俗易懂的教程.
𝔻ialogue
A: 我最近开始学Python了.
B: 好啊, 你都学了什么?
A: 我学了Python可以读作/ˈpīˌTHän/, 也可以读作/ˈpīTH(ə)n/, 是蟒蛇的意思...
B: 嗯, 还有呢?
A: uhmm... 还有变量的定义是变量是存放数据值的容器. 与其他编程语言不同, Python 没有声明变量的命令. 首次为其赋值时才会创建变量.
B: 不要背诵定义. 精确的定义毫无意义.
A: 那该怎么办?
B: 从例子中出发, 就把它当做英文说明书, 另外参考官方教程, 并且跟着官方教程做, 就会有大概的认识. 慢慢的, 你就能够得到你自己的定义了.
所以, 请认真阅读并实践(无论是在脑子还是在交互器(interactive shell)里面)官方帮助文档(可以在 https://docs.python.org/zh-cn/3/tutorial/introduction.html找到)1 的内容. 可以让你了解更多易于理解的东西. 如果文章中有描述C和Pascal的句子, 忽略它就可以. 毕竟文档是给各个不同层次和水平的人看的, 有一些看不懂以后再说.
𝕀dea
摒弃“我一定要一次把所有的东西都弄懂”的理念, 因为这些知识十分的巨大. 所以先了解一部分作为正确的立足点, 然后慢慢扩大就行了. 这需要很长时间的积累, 千万不要急. (着急也没用, 只会加大精神内耗.)
下面的内容其实不用单独记忆, 只要明确有哪些语句, 这些语句造成的效果是什么就行了. 如果看到有任何的问题, 如果是关于英语单词的, 可以搜索字典; 如果是对于程序报错有疑问, 可以搜索文档里面关于报错的信息; 如果有其他创造性的问题, 则可以询问周围的同学和老师.
下面会有两个术语(term), 分别是表达式(expression)和过程(procedure), 表达式可以暂且认为是形如x+12, [2]*3这样的可以进行计算的内容, 过程就是一系列执行的过程, 不一定要能得到值. 我们用一个例子感受一下.
def InsertionSort(A):
for j in range(1, len(A)): #Proc
key = A[j] #A[j],key are expr #Proc #|
i = j - 1 #j-1,i are an expr #v #|
while (i >=0) and (A[i] > key): #|
# <-expr-> <----expr-----> #|
# <-----------expr-----------> #|
A[i+1] = A[i] #A[i]is expr #Proc #|
i = i - 1 #i-1 is expr #v #|
A[i+1] = key #v
<-expr-> <-expr->
其实上面的Proc表示过程, 然后右边的是一个字符画, 表示↓, <-expr->其实表示的意思是expr这一段是表达式.
𝕀dea
早期的电脑只有80 ×24个只可以显示26个英文字母的黑白屏幕. 当时很多结构的图示就是通过像上面一样的字符画表示出来的.
重要的是, 把示例代码放到上面提到的可视化网站里面看一看就会很清楚, 很多概念都是不用记忆的.
语义: 看看有没有叫变量名的盒子, 如果有, 就把右边的内容计算出来重新把新东西替换进原来的盒子里; 否则, 就创建一个新盒子, 把右边算出来的东西丢进去.
下面我们给出注解:
b=114514
a=b+1 #执行完本句之后a=114515
b = b+1 # 执行完本句之后b=114515, a=114515不变
a = b+1 # 执行完本句之后a=114515, b=114516
a=”Fuhai Zhu teached Advanced Algebra” # a现在是字符串
a=1 # a现在是整数
a=None # None是一个关键字, 表示什么都没有.
print(a+1)
^
Traceback (most recent call last): File "<stdin>", line 1, in <module>
NameError: name ’n’ is not defined
(命名错误: 名称’n’没有定义)
𝔹onus
什么是Traceback? stdin又是什么? 后面会学习.
可以把什么东西放到盒子里面呢? 数字、字符串、列表. 当然这份回答相当不全面. 这时候可以参看官方文档 https://docs.python.org/zh-cn/3/tutorial/introduction.html来继续.
1.4.2. (条件判断) 可以使用if语句进行条件判断, 一般的, 有如下的形式:
if 表达式1:
过程1
elif 表达式2: # 可以有零个或者多个elif, 但是else后面不能有elif
过程2
else:
过程r
语义: 它通过逐个计算表达式, 直到发现一个表达式为真, 并且执行使表达式为真的这个过程(完成后不执行或计算if语句的其他部分的判断表达式) . 如果所有表达式都为false, 如果存在else下方语句块的过程.
下面我们同样给出注记和例子.
if "AK":
print("AK") # 会输出AK, 这是怎么判断的?(后续会回答)
zgw = 0
kertz = 1
ak = 1
cmo = 1
if kertz and ak and cmo :
print(“Zixuan Yuan got full mark in CMO”)
elif zgw and ak and cmo:
print(“zgw got full mark in CMO”)
else:
print(“zgw is such a noob”)
# 会输出Kertz got full mark in CMO, 由于已经找到了一个表达式的值为真的
# 表达式, 所以执行完print(“Zixuan Yuan got full mark in CMO”)之后就
# 会跳转到这个语句块的尾部了. 不会执行print(“zgw is such a noob”).
# (为自己菜爆的数学基础做了一个掩盖(大雾))
例子1.py-------------
if True:
print("Err")
----
File "main.py", line 3
print("Err")
^ IndentationError: expected an indented block
(缩进(indent)错误: 我预期有一个带着缩进的语句块, 但是没有)
例子2.py---------------
if False:
print(1)
else:
print(2)
elif True:
print(3)
---
File "main.py", line 5
elif True:
^ SyntaxError: invalid syntax
(语法错误: 无效的语法)
语义: 这样反复测试表达式, 如果为真, 则执行过程1如果表达式为假(这可能是第一次测试) , 则执行else子句的过程2(如果存在的话) , 然后循环终止. 在过程1中执行的break语句会终止循环, 且不执行else子句的过程2. 在过程1中执行的continue语句跳过过程1的continue语句之后的其余部分, 然后立刻回到测试表达式语句.
有了循环(loop), 我们就可以解读这个东西:
def InsertionSort(A):
j=1
while(j<len(A)):
key = A[j]
i = j - 1
while (i >=0) and (A[i] > key):
A[i+1] = A[i]
i = i - 1
A[i+1] = key
j=j+1
return A
InsertionSort([1,1,4,5,1,4])
这个程序做的事情就和排序成绩类似. 输入一个列表A, 它就可以把A进行排序.
(1) 执行到了最后一条语句, 没有下一条语句可以执行;
(2) 程序有没有被处理的异常(通常就有一个红色的报错了);
(3) 通过语句exit(0)退出.
因此, 我们就得到了最小的可以(理论上)执行任何与人类计算能力等价的模型
这些内容看上去十分的平凡, 但是通过一些过程的复合, 我们就能看到更多的魔力.
𝔻ialogue
A: 什么是复合? 我学过函数的复合, 但是感觉这里的复合还不太一样.
B: “复合”的方法可以分别列举, 也可以嵌套. 在上面的内容就有一些例子. 仔细体会这种过程.
A: 我不理解把两个循环变量嵌套该怎么体现.
B: 对于循环变量的嵌套可能一开始不是很好理解. 就想着有一根针指着当前要取的变量, 执行完当前过程, 想要执行下一步之后对应的针往后移动一位, 并且把所有的变量替换成针所指向的内容就行了.
我们可以把相似的过程写在一起, 为了简洁和可维护.
下面, 可以阅读https://docs.python.org/zh-cn/3/tutorial/controlflow.html#defining-functions 的4.7, 4.8.1-4.8.6节的内容, 把所有代码是怎么执行的放在pythontutor里面模拟着看一遍. 文字可以不用看, 但是代码一定要执行一遍.
观察下面的代码, 可能难以想象是怎么执行的:
def fib(n):
if(n==1):
return 1
if(n==2):
return 1
else:
return fib(n-1) + \
fib(n-2)
fib(5)
像这样用自己调用自己的函数调用通常叫做递归. 一个关于递归的有趣定义是:
事实上, 我们可以把它放在pythontutor里面执行一下, 发现如下的规则:
看上去就像是:
像羽毛球球桶那样, 只能从一个方向插入, 弹出的内容的东西叫做“栈(stack)”, 由于这些内容通常都是一些数据, 由此我们用术语数据结构(data structure)来描述. 能被取出来的那个元素是栈顶(top of the stack), 在这个可视化工具里面用蓝色标示出来了.
Traceback就是出错之后, Python顺着栈一层一层找的结果. Trace是跟踪, back是返回, 意思可能就是说堆栈的回溯(traceback).
下面我们来看一些基础的例子, 来体会上一节中的一些思考:
1def getpercent(chinese, math, english): 2 return (chinese+math+english)/(150+150+150) 3 4print(getpercent(100, 120, 135))
𝔹onus
如何判断一个程序的行为(behavior)? 为了刻画程序的行为, 我们能不能像第一节里面提到的那样, 用一个“模型(model)”来描述它?
宏观来说, 程序就是状态机. 程序的执行就是状态的迁移(transform). 到底有哪些状态呢?
1money = [10, 14, 13, 10] 2int total = 0 3for i in money: 4 total = total + i 5 6print(money)
这里的for i in ...只是for u in range(len(money)), i=money[u]的简称罢了. 对我们的实际程序没有太多的障碍. 还是逃脱不了循环的大框架. 我们在前面说的最小指令集还是起作用的.
1def isprime(x): 2 flag = 1 3 d=2 4 while d<x: 5 if x%d == 0: 6 flag = 0 7 d = d+1 8 if flag: 9 return 1 10 else: 11 return 0
在这个程序片段中, flag 代表了什么? 是不是有些像现实世界中的信息传递方式? 因为我们无法跨越循环次序改变程序的行为, 我们只好使用变量flag来记录, 并且让程序的控制流通过flag来进行判断与执行.
𝔹onus
素数(prime)有什么数学性质? 我们是用什么性质来判定性质的? 在我们下达的指令里面, 形式上和数学表达式相似吗?
事实上, 数学上的定义是∀x,¬∃p,s.t.p|x. 我们的程序看上去并不是像数学那样简洁. 其实, 程序设计家族也有其他成员可以写起来比较优美.
ℙassage
程序设计家族的其他成员: 不只有下达命令
南京大学 李樾(见图1.2)等 节选自《程序分析》教科书
在IP中指令一个一个给出用条件、循环等来控制逻辑指令执行的顺序同时这些逻辑通过程序变量不断修改程序状态最终计算出结果。我觉得尽管IP现在都是高级语言了但是本质上并没有脱离那种“类似汇编的通过读取、写入等指令操作内存数据”的编程方式我后面会提及这是源于图灵机以及后续冯诺依曼体系结构一脉的历史选择。国内高等教育中接触的绝大多数编程语言都是IP的比如Java、C、C++等。
在FP中逻辑用函数来表达可以像数据一样抽象起来复杂的逻辑高阶函数可以通过操纵传递、调用、返回简单的逻辑低阶函数和数据来表达没有了时序与状态隐藏了计算的很多细节。不同的逻辑因为没有被时序和状态耦合在一起程序本身模块化更强也更利于不同逻辑被并行的处理同时避免因并行或并发处理可能带来的程序故障隐患这也说明了为什么FP语言如Haskell在金融等领域高并发且需要避免程序并发错误受到瞩目。
1 (defun quadratic-roots-2 (A B C) 2 (cond ((= A 0) (string "Not a quadratic equation.")) 3 (t 4 (let ((D (- (* B B) (* 4 A C)))) 5 (cond ((= D 0) (concatenate ’string "x = " (write-to-string (/ (+ (- B) (sqrt D)) (* 2 A))))) 6 (t 7 (values (concatenate ’string "x1 = " (write-to-string (/ (+ (- B) (sqrt D)) (* 2 A)))) 8 (concatenate ’string "x2 = " (write-to-string (/ (- (- B) (sqrt D)) (* 2 A)))))))))))
LP抽象的能力就更强了(用逻辑来表达)计算细节干脆不见了。把你想表达的逻辑直观表达出来就好了如“第三代火影的徒弟” 且 不是“女性” 且 “其徒弟也是火影”=>”自来也“。嗯学会”与或非“编程都不怕。 如今在数据驱动计算日益增加的背景下LP中的声明式语言Declarative programming language如Datalog作为代表开始崭露头角在诸多专家领域开拓应用市场。我们这本小书也准备用一章节来教大家如何使用Datalog语言编写程序分析器。
1ancestor(A, B) :- 2 parent(A, C), 3 ancestor(C, B). 4
1def is_perfect(n): 2 sum=0 3 for i in range(1,n): 4 if n%i==0: 5 sum=sum+i 6 return sum==n
其中range现在可以认为是生成[1,n)的列表. 并且每一次循环就取列表的下一个元素. 比如for i in range(1,5)每次循环i的值会是1 2 3 4.
在这个实例中, 逻辑关系体现的如何?
1def multiples_of_3_and_5(n): 2 sum=0 3 for i in range(1, n): 4 if i%3==0 or i%5==0: 5 sum=sum+i 6 return sum
可以注意我们的逻辑在Python里面是如何表达的? 还有哪些逻辑表达关系? 事实上, 这也是后续离散数学部分要学的命题逻辑–我们需要对于以前的逻辑有一个比较确切的定义.
𝔹onus
命题“若p则q”的否定是什么?
普通的高中毕业生基本是无法回答这个问题的. 因为课本的知识完全没有提及类似的问题. 这就导致我们的高中数学看上去更像是民科学习的数学. 同时轻松地毁掉了高中与大学的衔接过程.
1def integer_right_triangles(p): 2 # a^2+b^2=c^2 a+b+c=p c is the longest 3 count=0 4 for a in range(1,p): 5 for b in range(a,p-a): 6 c=p-a-b 7 if a+b+c==p and a**2+b**2==c**2: 8 count+=1 9 print(a,b,c) 10 return count
这个例子对于数学的关系好像更加清晰了. 比如直角三角形数对有兴致a2 + b2 = c2. 于是剩下的就比较像自然的“数数”一样了.
1def fib(n): 2 if(n==1): 3 return 1 4 if(n==2): 5 return 1 6 else: 7 return fib(n-1) + \ 8 fib(n-2) 9 10fib(5)
这个内容也在前方的例子中有提及, 这样我们自然的就得出了“栈”的定义. 这也是我们这里接触的第一个数据结构–栈.
𝕀dea
计算机高级程序可以由较为低级的程序解释. 这种程序一般而言更加机械, 但是更不利于我们的问题的解答. 这就需要一层一层的抽象叠加起来.
如果自己曾经动手写过一点代码的话, 我们就会发现把代码调试对是一件很不容易的事情. 下面我们给出一些小提示:
(1) 阅读程序的报错信息. 我们发现很多同学会对于红色的Syntax Error如临大敌, 见到就跑. 下面, 我来举一个例子来说明为什么这是对的:
𝔻ialogue
A: 我将会按照一定的规则给出三个数字, 我想让你找出这个规则是什么. 但是你能够获取信息的途径是: 你自己再列举三个数字. 我会告诉你这列数字是不是符合我的规则. 然后你们就可以说出来你们认为的规则是什么.
B: 好的, 明白了.
A: 我说出来的三个数字是2, 4, 8.
B: 我猜测16,32,64.
A: 符合我的规则.
B: 那我想规则是2n.
A: 其实并不是这样.
为什么会出现这样的情况? 这就是因为没有知道什么东西是“错的”. 请观看真理元素的《你能解决这一问题吗》视频, 思考一下为什么错误也是很重要的. 这位UP在B站上的官方中文翻译视频链接是 https://www.bilibili.com/video/BV1Hx41157jV.
(2) 程序出现难以预料的行为时, 在脑子里面模拟执行一遍程序. 告诉自己“程序就是状态机”. 看一看逻辑设计的是不是出错了.
(3) 善于使用调试器. 观察程序在哪一个地方与你预期的执行不相符. 这时候, 往往就意味着可以提问了.

ℙassage
与其说是学会提问, 倒不如说是学会不提问
南京大学 蒋炎岩
中国科学技术大学 余子豪(图1.3)
节选自《PA实验手册》
很多同学不多不少都会抱有这样的观点:
我向大佬请教, 大佬告诉我答案, 我就学习了.
但你是否想过, 将来你进入公司, 你的领导让你尝试一个技术方案; 或者是将来你进入学校的课题组, 你的导师让你探索一个新课题. 你可能会觉得: 到时候身边肯定有厉害的同事, 或者有师兄师姐来带我. 但实际情况是, 同事也要完成他的KPI, 师兄师姐也要做他们自己的课题, 没有人愿意被你一天到晚追着询问, 总有一天没有大佬告诉你答案, 你将要如何完成任务?
如果你觉得自己搞不定, 你很可能缺少独立解决问题的能力.
但幸运的是, 这种能力是可以训练出来的. 你身边的大佬之所以成为了大佬, 是因为他们比你更早地锻炼出独立解决问题的能力: 当你还在向他们请教一个很傻的问题的时候, 他们早就解决过无数个奇葩问题了. 事实上, 你的能力是跟你独立解决问题的投入成正比的, 大佬告诉你答案, 展示的是大佬的能力, 并不是你的能力. 所以, 要锻炼出独立解决问题的能力, 更重要的是端正自己的心态: 你来参加学习, 你就应该尽自己最大努力独立解决遇到的所有问题.
很多问题都可以通过查资料解答. 其中, 有一个很好的途径就是先看一看官方文档. 通常官方文档都有非常详细的解释.
1.1_____________________________________________________________________________
一个很好玩的事情是, C语言程序设计的基本语法比Python更加的基础. 而且C基本代码的语义的确定的掌握要花费的精力是远远小于Python的. 它更简单、包袱更少也没有很庞大的工具链。虽然说这相当于 “把你的手脚捆起来编程”但我们通常不需要很复杂的数据结构和代码逻辑因此现代语言特性的好处在大部分时候并不显著。而且用 C 语言还有一些额外的好处
和其他编程语言相比,C 语言特性更容易真正掌握和深入理解.如果你没有学好,用几周的时间补上应该也没问题 C 是一种 “高级的汇编语言”, 你不难在大脑里把 C 出代码翻译成指令序列; 但对于现代语言来说, 这要困难得多. 透过对 C 语言的深入理解, 可以更好地理解现代编程语言的设计动机和实现方法.
–蒋炎岩, 操作系统课程自救指南
所以, 不用惊慌. 我们会来简单介绍一下. 我们会用几个例子来说明一下C语言里面, 一些规则. 但是不用试图记忆, 最好能够跟着敲一遍. 一个比较完好的编译器会在你犯错误的时候(通常情况下犯错是很正常的)给出你提示. 这时候查一查字典就可以解决大多数的情形.
作为计算机, 一个很重要的事情是: 如何使用计算机进行比较复杂的算术运算?
比如下面的程序可以告诉我们1+1的值, 并且输出到屏幕.
1#include <cstdio.h> 2int main(){ 3 printf("%d\n", 1+1); 4 return 0; 5}
这里的“%d”是输出的占位符, 会输出整数. d是digit的简称. 因为整数是由一位一位的数码构成的.
我们来看一看有没有什么有趣的实验:
𝔼xample:
修改程序, 输出(1) 3 −4; (2) 5 ×6; (3) 8 ÷4; (4)8 ÷5的值.
和Python不同, C会默认地把1.6转化成整数. 这是为什么?
ℙassage
(Generated from ChatGPT)
In the early days of computing, hardware resources were limited, and memory and processing power were at a premium. The ability to perform automatic conversions between different data types was therefore an important feature of programming languages, as it allowed programmers to work with limited resources more efficiently.
Additionally, the automatic conversion of float to int likely reflects the fact that early computer hardware often did not support floating-point arithmetic natively. Floating-point arithmetic was typically implemented in software, which was slower and less efficient than the native integer arithmetic. Therefore, it was often necessary to convert floating-point values to integers in order to perform arithmetic operations more efficiently.
As hardware capabilities have evolved over time, the automatic conversion of float to int in C has remained an important feature, as it provides a convenient way to work with different data types and to simplify code. However, it’s still important for programmers to be aware of the potential loss of precision when converting between data types, and to use these conversions intentionally and with care.
对于实数, 我们可以使用%f输出. f是float的简称, 用来表示这是一个浮点数(也就是实数, 因为小数点会“浮动”).
𝔹onus
C是一个强类型的语言–也就是每一个变量都有一个一旦声明不能更改的类型.
如果我们输出8/5.0, 用%f和%d输出有什么区别? 在输出的过程中你认为的类型变换的过程如何?
如果我们在程序的开头加上#include <math.h>, 就可以得到更加多样的数学运算. 如: 要计算1 + 2 _
5−0.1, 我们就可以在main()里面替换上
1 printf("%.2f\n", 1+2*sqrt(3)/(5-0.1));
𝕀dea
理解代码的核心方法(上): 像阅读数学公式那样, 通过代换法理解一行代码.
举个例子, 我们在理解上面的内容的时候, 可以拆分成若干个部分, 想一想每一部分做了哪些输出. 最后整合起来就好了.
我们上面已经可以计算东西了, 可是还是不够劲啊! 如果我们能够从键盘读取输入就更加不错了! 那我们就需要用到scanf了.
输入的东西放在哪里呢? 可以放在小盒子里面. 和Python的“小盒子”不是很相同, 小盒子必须指定变量, 并且指定了之后不能修改盒子的类型. 这也是历史上的因素导致的.
我们来试一试: 比如最简单的a + b问题: 输入两个数, 用程序把它求和, 结果输出出来.
1#include <cstdio.h> 2int main(){ 3 int a, b; 4 scanf("%d%d", &a, &b); 5 printf("%d\n", a+b); 6 return 0; 7}
这时候, 代换的方法仍然起作用. 我们就可以通过交互的情况下得到输入与输出了!
回忆一下小学的时候, 我们总是被要求计算(有点无聊的)圆柱体的表面积. 如果有一个小程序可以帮助当时的我们, 输入半径和高, 自动为我们输出答案, 那样自己就很好了. 于是我们有:
1#include <stdio.h> 2#include <math.h> 3int main(){ 4 const double pi = 3.14; 5 double r, h, s1, s2, s; 6 scanf("%lf%lf", &r, &h); 7 s1 = pi*r*r; 8 s2 = 2*pi*r*h; 9 s = s1*2.0 + s2; 10 printf("Area = %.3f\n", s); 11 return 0; 12}
上面我们编写了很多行的代码, 一个问题是我们的程序是怎样被执行的? 事实上, 这点和Python区别不大–在没有控制执行的情形下都是顺序–从上到下一行一行执行的. 我们可以使用调试器来证明这一点.
𝕋ools
根据观察, 有很大一部分学生甚至不知道调试器是什么! 这件事情是很糟糕的–因为这样下来很多时候就会让他们看程序“一头雾水”, 然后这就是放弃的前兆.
所以个人认为作为一个很重要的工具–调试器在刚开始的时候就应该介绍一下. 这个工具可以帮助我们看到计算机里面到底发生了什么, 从而理解我们的输入到底在干什么. 我们可以为我们的程序打上断点(breakpoint), 然后启动调试–程序就会自动停下了, 同时把现在的状态告诉我们.
我一直一来是不太赞成初学的时候使用Python的语法特性a, b = b, a来做交换变量的. 其原因是可能会让一部分关键的直觉和感受丢失. 比如, 如果我们在C中希望交换两个变量, 怎么办?
如果我们还想像Python那样, 看一看会得到什么:
1$ vim tmp.c 2 3#include <bits/stdc++.h> 4int main(){ 5 int a = 1, b=2; 6 a, b = b, a; 7 printf("a=%d, b=%d", a, b); 8 return 0; 9} 10 11:!gcc %.c 12 13warning: left operand of comma operator has no effect [-Wunused-val 14ue] 15 a, b = b, a; 16 ^ 17tmp.cpp:4:15: warning: expression result unused [-Wunused-value] 18 a, b = b, a; 19 ^ 202 warnings generated.
哦, 出警报了, 我们看一看运行之后会有什么效果:
1:!./a.out 2a=1, b=2
诶, 完全没有效果了! 我们回顾上面的警告说这句话没有任何的作用. 这样就解释了这件事. 所以我们要用更加底层的方法来完成.
我们现在有哪些工具呢? (1) 创建一个带有类型的盒子; (2) 为这个盒子装/修改东西; (3) 输入, 输出; (4) 新增一行(句)代码.
我们刚刚对于所有的东西这样描述不够劲啊, 毕竟我们还是只是一个一个地完成步骤的说明. 有没有方法完成自动的重复呢? 我们可以用while循环.
那么如果我们希望在某一个地方就不用继续循环下去了, 可以用break; 如果在某一个地方跳过下面的语句继续循环, 那么可以用continue.
与while相仿, 我们还可以用for循环. for的语法比较像∑ . 同样也有break和continue.
如果我们想要创建100个变量, 我们可以不用声明a0, a1,a2,... . 我们有可以自动给一个“空间”, 就像int a[100];, 这样就给我们了100个变量的int类型的空间. 如果我们想访问其中的一个(比如第14个), 我们就可以用a[14]来访问. 注意: 数组从0开始编号, 访问a[100]虽然不会有报错信息, 但是这是未定义行为.
我们可以用重复的方法来走遍一个数组里面的所有的部分. 可以和上面的for很方便的对应起来.
当然我们还可以创建多个方括号, 简称为“维度”. 比如b[100][100就可以让我们在一个100 ×100的平面上面读取数据. 比如想访问第二行(从0计数)第三列(从0计数)的就可以写成b[2][3] 当然, 这个维度可以是任意多个的–只要不超出内存限制就没问题.
这证明了一个普遍规则程序帮你写的代码会比你自己手写的更正 确、更可靠。如果改进了生成器例如能生成更好的代码那么每个人 都会受益相反对手写程序的改进并不能改善其他程序。像Yacc和 Lex这样的工具是这一规则的极好例子Unix也提供了许多其他工具。 编写程序的程序总是值得尝试。就像道格·麦基尔罗伊所言“任何你必 须重复做的事都有待自动化。” – Unix传奇: 历史与回忆
“有两种推广一种没有什么价值, 另一种则是有价值的没什么思想、仅凭唬人的专人术语做推广是很容易做到的颇为困难的是从若干好的素材中提取出一份精致凝练的精品.” —- George Polya
𝔻ialogue
A: 问一个这一章比较简单a 的问题: 如果我有一个命题叫做“若p则q”, 那么这个命题的否定是什么?
B: 我研究这个干什么? 闲着找事情吗?
A: 想一想你学习的极限理论. 如果我希望对于“一个数列的极限存在”这个事情做否定, 你会怎样否定?
B: 数列极限的定义是如果一个数列的极限是 A , 那么就是说∀n > N,∃|𝜖|≥0,s.t.|an −A|< 𝜖. 要是否定还是真的不是一件容易的事情啊...
A: 这就是我们学习命题逻辑的原因. 以后我们会遇见成百上千的命题等待我们的操作, 如何从中找到逻辑就至关重要.
事实上, 很多同学是在学习数学中体会到逻辑的. 但是, 我们当中的很多人会发现: 数学仅仅是为了对付高考这样的考试. 那么希望在这一节以及以后的生活中, 慢慢体会数学带给我们的潜移默化的影响.
这一部分我们建议参看教科书《Reading, Writing, and Proving A Closer Look at Mathematics》的第一章. 我们会在这一章主要概括一下它的主要意思. 由于是为了本科生写的数学课本, 所以句子十分的容易懂. 就当做一个小练习吧.
2.1.1. 结合自己的数学学习经历, 阅读《Reading, Writing, and Proving A Closer Look at Mathematics》的第一章, 然后与下文进行比对. 看一看自己的英语理解能力如何. 不设置时间限制, 因为我们需要做的是尽可能的联系自己过去的数学学习经历, 然后去体会这段文本.
我们在生活中经常看到这样的对话:
𝔻ialogue
学那么多的数学有什么用? 买菜又用不到这样的数学, 学这些还有用吗?
再后来, 我们发现所有的数学问题都可以通过一种“程序化”的手段来解决. 比如, 我们在上一学期学习的Gram-Schmidt正交化矩阵向量的基、解其次线性方程组、求导数等等这样的操作, 都有一系列的明确的步骤.
那么数学仅仅是局限于此吗? 我们来看一看那些伟大的数学家的思想是什么样的:
伟大的数学家、教育学家George Polya专门出了一本书叫做“如何解题”. 于是, 学习数学一个很重要的目的可能就是教会我们:
(1) 如何解决一个问题;
(2) 为什么这样做是对的;
(3) 这个方法什么时候是对的.
𝔼xample:
我们是如何解含有未知数的等式(通常叫为方程), 其中一个比较重要的方法是消去律.
对于实数构成的方程, 消去律大多数都是成立的(只要等式两端不除以0), 但是对于含有未知矩阵的方程, 这样的方法很多时候就不灵了.
在我们遇到一个难以解答的数学问题的时候, 还是回过头来看看George Polya为我们总结的How to solve it的一个list吧.
ℙassage
How to Solve it
Summarized text
Originated from George Polya’s How to solve it
First, you have to understand the problem.
"Understand the problem" is often neglected as being obvious and is not even mentioned in many mathematics classes. Yet students are often stymied in their efforts to solve it, simply because they don’t understand it fully, or even in part. In order to remedy this oversight, Pólya taught teachers how to prompt each student with appropriate questions, depending on the situation, such as:
What are you asked to find or show?
Can you restate the problem in your own words?
Can you think of a picture or a diagram that might help you understand the problem?
Is there enough information to enable you to find a solution?
Do you understand all the words used in stating the problem?
Do you need to ask a question to get the answer?
The teacher is to select the question with the appropriate level of difficulty for each student to ascertain if each student understands at their own level, moving up or down the list to prompt each student, until each one can respond with something constructive.
Second principle: Devise a plan:
Pólya mentions that there are many reasonable ways to solve problems. The skill at choosing an appropriate strategy is best learned by solving many problems. You will find choosing a strategy increasingly easy. A partial list of strategies is included:
Guess and check, Make an orderly list, Eliminate possibilities, Use symmetry, Consider special cases, Use direct reasoning, Solve an equation
Also suggested:
Look for a pattern,Draw a picture,Solve a simpler problem,Use a model,Work backward,Use a formula, Be creative.
Applying these rules to devise a plan takes your own skill and judgement.
Polya lays a big emphasis on the teachers’ behavior. A teacher should support students with devising their own plan with a question method that goes from the most general questions to more particular questions, with the goal that the last step to having a plan is made by the student. He maintains that just showing students a plan, no matter how good it is, does not help them.
Third principle: Carry out the plan
This step is usually easier than devising the plan.[23] In general, all you need is care and patience, given that you have the necessary skills. Persist with the plan that you have chosen. If it continues not to work, discard it and choose another. Don’t be misled; this is how mathematics is done, even by professionals.
Fourth principle: Review/extend
Pólya mentions that much can be gained by taking the time to reflect and look back at what you have done, what worked and what did not, and with thinking about other problems where this could be useful. Doing this will enable you to predict what strategy to use to solve future problems, if these relate to the original problem.
在解答完这些问题之后, 我们往往会感到满足. 很多时候这也是我们去学习数学的一个很重要的原因.
𝔻ialogue
A: 可我一点感觉开心也没有啊!
B: 可能是把做题看得太重了. 高考的“把题目作对”的观念在大学里面就应该淡化掉了.
A: 此话怎讲?
B: 来看一看朱富海老师的文章就知道了.
ℙassage
高中数学与大学数学
南京大学 朱富海(图2.1) 节选自数林广记微信公众号
美国大学的数学研究者们对于学生包括中学生的培养的确非常有热情, 比如一些名校的博士生在暑假期间常常有打工的机会, 主要任务是指导一些高中生尝试做科研. 2011 年, MIT 的 Pavel Etingof 教授与另外六位作者合作出版了一本书, 题目是 Introduction to Representation Theory.
这本书的内容包括代数、有限群、quiver箭图表示论, 以及范畴论和有限维代数结构理论, 其中的大部分内容在国内高校数学院系的本科甚至研究生课程中都讲不到. 在 Etingof 的主页可以找到这本书的 PDF 文档. 他在前言中说, 这本书是他在 2004 年给其他六位合作者的授课讲稿, 而这六位听众当时都是高中生! 其中的 Tiankai Liu 应该是华人, 在 2001, 2002, 2004 年三次代表美国队参加国际数学奥林匹克都获得金牌. 还有一位合作者是来自 South Eugene 高中的 Dmitry Vaintrob, 他在 2006 年获得面向高中生的 Siemens 竞赛的第一名, 论文题目是 The string topology BV algebra, Hochschild cohomology and the Goldman bracket on surfaces, 论文已经涉及到很深的数学理论, 在 Dmitry Vaintrob 的主页上也能找到.
再看看我们在做什么? 曾经看过一道竞赛训练题, 其本质是把八位数19101112华罗庚先生的诞生日分解质因数. 很容易找到因数 8, 然后就一筹莫展了. 后来借助网络工具才直到 19101112 = 8×1163×2053. 看到结果有点傻眼了: 有谁能只用纸笔得到这个分解? 后来发现自己孤陋寡闻了, 有学生说这种分解质因数早就背过! 细细一想真的极为恐怖: 他们为什么要背这个? 他们又背了多少类似的东西?
想想挺有意思: 杰出的数学家们用他们的智慧和汗水去探索和展现数学之美, 而我们花费了大量时间和脑细胞记忆一些很容易遗忘的意义不大的知识点, 轻轻松松地毁掉数学之美的同时顺便浇灭了学生们的求知欲.
𝔻ialogue
(...对话仍在继续...)
B: 所以嘛, 我们只要把高考带来的陋习去除掉就行了. 也就是所谓的“去高考化”.
A: 听起来确实很有希望. 我们终于不用再整天因为分数担惊受怕了.
B: 是的, 但是看起来我们都是在这份讲稿里面存在的人物. 希望我们的存在能够对现实世界的你有一定的帮助吧.
同样, 顺着南京大学的问题求解课程, 我们同样找到了一本很有趣的书: 《Mathematics: A Discrete Introduction, Second Edition. Edward R. Scheinerman》. 这本书里面详细讲述了我们为什么要学习数学, 以及数学学习带来的享受.
𝔻ialogue
A: 为什么不让我读第六个小节?
B: 这是因为嘛... 第六小节就是我们下一节课的内容了.
A: 太好了, 我要预习!
B: 这时候终于知道了高中老师说的“预习”的重要性了吧!
A: 确实, 这样一来确实切身感受到了预习的重要性. 这样做可以帮助我了解我的理解哪里出了问题, 于是就可以更加准确地向老师发问, 而不必纠缠于那些可有可无的奇怪问题了.
我们先来看存在于大学数学课本的很多重要的元素和栏目.
定义的结构通常形如: X是一个具有性质Y的东西. 其实, 很多情形下, 我们对于定义的理解是很需要时间的, 一般地, 我们需要关注:
𝕀dea
对于数学定义, 我们需要关注如下的几个问题:
命题是我们关于数学对象的一些陈述性的性质. 那些陈述性的性质, 如果命题是真的, 我们就称为真命题(有些难以得到的也称作“定理”); 不知道是不是真的命题一般来称为猜想; 错误的命题通常就称为“错误”.
数学中的命题和物理里面的命题有什么不同点? 比如, 我们说Galileo的速度变换公式在低速的情形下是成立的, 当速度接近光速c的时候, 这个公式就不灵了. 换言之, 我们只是使用了一个近似的表达结果. 但是, 数学的逻辑世界中这样的事情是不会发生的. 我们如果认为一个“命题”是真的, 那么在给定公理体系下, 无论什么情形下, 都是对的.
通常描述一个命题的时候, 我们使用的是若p则q的形式来完成表述. 那么什么叫做“若...则...”呢? 其实它的意思是对于任何一个真的p, q一定是真的. 具体的关系可以参看表格2.1.
𝔹onus
若p则q还有哪些等价的表示形式? 英语里面有哪些表达方式? 是不是比中文更加自然了?
2.1.3. 用“当且仅当”写出的类似表2.1的表格.
关于逻辑连接词, 我们会在后面专门讨论. 下面再来看几个名词. 从上述参考资料中直接摘录了部分结果.
这个用的就比较多了. 我们曾经学过很多的方法, 比如反证法, 数学归纳法等.
𝔹onus
为什么这些东西是对的? 例如, 我们为什么不能用数学归纳法证明含有ℝ为变量的命题? 可以使用数学归纳法证明关于无穷的证明吗?
𝔻ialogue
A: 为什么采用符号化的方法? 用自然的语言不是更方便吗?
B: 这个视频可能是给出了一个答案, 里面提出了一些历史.
(数学有一个致命的缺陷 约40分钟 https://www.bilibili.com/video/BV1464y1k7Ya/ )
A: 我们还要符号化更多的东西吗?
B: 当然! 后面我们的抽象层次还会进一步加深. 只有在前面的抽象领域打好坚实的基础, 才可以学得动下面的内容!
A: 举个例子?
B: 现在让你去给刚学完加减乘除的小学生讲数学分析, 能在一个下午让他写出来很好的证明吗?
A: 这当然不行. 可能是没有受到一些理论的熏陶, 训练时间不是很足.
B: 确实是这样的. 在下面的命题逻辑和谓词逻辑中, 我们会像程序设计语言那样, 关注命题逻辑和谓词逻辑的语法和语义.
𝕀dea
以下是下面的内容的路线图.
![]()
等价变形关注的是一个公式内部简化与变形, 推理关注的是公式与公式之间的关系.
从高中开始, 我们似乎就开始处理各种各样的命题. 下面我们加一层抽象, 这样, 我们就可以把一些繁琐的内容交给计算机完成, 并且在探索的过程中对“什么是有效的推理”有一个更深的理解.
相仿地, 我们试图像第一章探求的“最小的指令集合”一样, 问一问: 我们表达的逻辑, 有没有一些基础的组成部分?
𝔼xample:
2.2.2 (命题逻辑的语法). 命题逻辑的语言有且仅有如下的内容构成:
| 符号 | 名称 | 英文读法 | 中文读法 | LaTeX |
| ¬ | negation(否定) | not | 非 | \lnot |
| ∧ | conjunction(合取) | and | 与 | \land |
| ∨ | disjunction(析取) | or | 或 | \lor |
| → | conditional | implies(if then) | 蕴含(如果, 那么) | \to |
| ↔ | biconditional | if and only if | 当且仅当 | \leftrightarrow |
𝔻ialogue
A: 为什么没有常见的“任意”, “存在”之类的量词?
B: 因为这样就复杂了. 包括结果判定的正确性和推理的难度上. 我们下一章会详细讲讲这个.
𝔹onus
为什么叫合取, 为什么叫析取?
其实命名的关键在于描述中的“和”和“析”. 我们可以查询古汉语字典来获取他们的意思. 并且从中找到一些合理性.
下面, 不妨用Python语言为例, 来看一看这些内容是如何在语言中有所设计的. 需要注意的是, 上表格中的后两个记号并不是新的. 只是我们经常用他们, 于是就变成了一个独立的记号.
如果p那么q的意思是: 如果p是对的, 那么q一定是对的, 如果p是错的, 那么q的真假性不确定. 因此, 我们可以把p →q表示为¬p ∨q–意味着要么p不成立, 要么当p成立的时候q是对的–命题只有对和错, 所以我们就很干净的进行了一次分类讨论.
当且仅当的表示就是“若p则q, 且若q则p”. 本质上还是命题符号之间的“非”, “或”, “与”之间的连接.
𝔼xample:
命题的真假在Python中可以用布尔表达式(boolean expression)的真(true)和假(false)表示. 比如今有变量a=True,b=False,c=True, 那么
1 a=True, b=False, c=True 2 var = a and b or not c 3 print(var) 4
打印的真值就是就是a ∧b ∨¬c的真值.
既然我们规定了符号, 自然要研究一下他们的运算律和运算关系. 什么是运算律?
𝔼xample:
我们从小就开始听到运算律的相关内容了. 那么什么是运算律? 某国外网站的解释如下.
The order of operations is a rule that tells the correct sequence of steps for evaluating a math expression. We can remember the order using PEMDAS: Parentheses, Exponents, Multiplication and Division (from left to right), Addition and Subtraction (from left to right).
但是我们还听说过“交换律(commutive law)”, “结合律(associative law)”这样的名词. 这些内容反应了我们可以如何书写, 如何计算一个表达式.

𝕀dea
除了这些, 对于命题, 我们需要了解这些四个内容:
一个可以判定“真/假”的“东西” – 命题
简单命题组成更复杂的命题 – 连接词
深入命题的内部 – 谓词与变元
体现“普遍性”与“存在性” – 量词
现在, 我们就可以探讨更多的语义相关的内容了. 来看一看能对这个公式产生怎样的解释.
2.2.3 (命题符号的运算规则). 一般地, 命题记号遵循如下的运算规则:
那么我们说的命题的真假是怎么界定的呢? 通常情况下, 我们需要分类讨论每一个需要讨论的命题的真假, 最后看一看根据公式表达的真假性就行了. 所以, 我们很多时候希望“假定”这些命题的真假, 来考察最终结论的真假, 并且希望从中找到一点规律. 这样做其实有一个更专业的名字叫“真值指派”. 这样我们就可以对于“这句话永远是对的”有一个更加深刻的定义.
𝔻ialogue
A: 我现在知道这些条件是, 对于明天高等数学课程的一些事情.
B: 什么事情?
A: 如果明天老师讲完了《空间立体几何》, 那么他就会做一个小测试. 同时如果我如果学的非常差的话, 并且旁边还没有大佬捞我的话, 我的平时分就非常惨淡.
B: 那我来分析一下, 假设老师没有讲完, 那么平时分暂时还不会受到影响; 如果老师讲完了, 同时我学得不差, 平时分也不会受到影响. 如果老师讲完了, 我学得非常差, 但是有人捞, 那么平时分也不会受到影响. 但是这是违反学术诚信的, 并不能做. 所以, 只要自己学得比较好才能得到很好的平时分.
像上面的例子, 我们通常会对命题的一些内容的真假进行预先假定, 即: 对于命题进行真值指派.
具体的, 我们可以“指派”命题符号中的各个变量的值, 然后映射到真或假两种情况.
我们可以借助这个想法为我们上面定义的为我们上面的逻辑连接词做一个精确的数学定义. 叫做“真值表”.
比如, 我们有“非”的真值表(表2.3)、“和”的真值表(表2.4)、“或”真值表(表2.5)、“若,则”真值表((表2.6)以及“当且仅当”的真值表(表2.7)
2.2.1. 人类学者埃贝尔考察一个有着许多古怪社会现象的群岛他到访的第一个小岛上的居民分为两类而且每人必属其中的一类:
在岛上埃贝尔遇到一行三人且称他们为 A, B, C。 埃贝尔问A: “你是knight还是knave?” A回答了但埃贝尔没听清 于是埃贝尔就问B: “他(A)说的是什么” B告诉埃贝尔A说自己是knave。
此时C插话说“别相信他(B)他说谎”
我们的问题是C是 knight 还是 knave?
事实上, 我们在小学很可能通过列举的方法完成求解. 但是现在我们可以用真值表列举. 甚至可以把公式写出来进行推演!
𝔹onus
等等, 什么叫推演? 有哪些推演规律? 这些推演规律是不是可以用公式表示? 这些都是下一节要介绍的内容.
比如一个命题的否定的否定还是原命题本身一样, 我们可以定义一些“公式”. 比如
p̸与p等价.首先我们定义一下什么叫“满足′′,“蕴含′′或者“等价′′.
很多时候一些逻辑表达式看上去就是废话. 比如“如果我后天知道了考试的成绩, 那我明天就知道了”. 数学上面对这类问题有一个定义叫做“重言蕴含”.
2.2.8 (重言式/永真式 (Tautology)). 如果将等价词两侧的子公式各自看作表达式则这两个逻辑表达式对于相关逻辑变量的任意赋值有相同的逻辑值.
(或者: 如果 ∅α, 则称 α 为重言式, 记为
α.)
反之, 就是永远都不能成立的矛盾的形式.
我们可以认为是语义上的, ⊢是 偏向语法上的推演.
对于命题公式而言, 如果对于相同的变量输入, 外部观测的结果的真假相同, 我们就称为命题的等价.
2.2.11 (命题的等价). 设G,H是两个命题公式,
P1,,Pn是出现在命题G,H中的所有变元, 如果对于P1,P2,
,Pn的2n组不同的解释, G,H的真值结果都相同, 那么称G和H是等价的,
记作G ⇔H.
根据上面的定义, 我们可以证明:
𝔹onus
永真式和等价有什么区别和联系?
A proposition that is always True is called a tautology. Two propositions p and q are logically equivalent if their truth tables are the same. Namely, p and q are logically equivalent if p ↔q is a tautology. If p and q are logically equivalent, we write p ⇔q.
在上面我们发现了有很多的“废话”, 但是, 当看上去是“废话”的东西堆多堆复杂的时候, 那么它就不是显然的. 这就需要一些推理规律来帮助我们联通看上去毫不相干的逻辑符号.
经过我们的探讨, 我们就希望把一些最基本的规律写出来:
利用这些内容我们可以构造一些等价的命题:
2.2.2 (基本等价定律). (1) 幂等律: E1 : G ∧G ⇔G;E2 : G ∨G ⇔G;
(2) 交换律: E3 : G ∧H ⇔H ∧G;E4 : G ∨H ⇔H ∨G;
(3) 结合律: E5 : G ∧(H ∧S) ⇔(G ∧H) ∧S;E6 : G ∨(H ∨S) ⇔(G ∨H) ∨S
(4) 分配律: E7 : G ∨(H ∧S) ⇔(G ∨H) ∧(G ∨S);E8 : G ∧(H ∨S) ⇔(G ∧H) ∨(G ∨S)
(5) 吸收律: E9 : G ∨(G ∧H) ⇔G;E10 : G ∧(G ∨H) ⇔G
(6) 同一律: E11 : G ∨False ⇔G;E12 : G ∧true ⇔G
(7) 零律: E13 : G ∨True ⇔True;E14 : G ∧False = False
(8) 双重否定律: E15 : ¬(¬G) ⇔G
(9) De Morgan律: E16 : ¬(G ∨H) ⇔¬G ∧¬H;E17 : ¬(G ∧H) = ¬G ∨¬H
(10) 矛盾律: E18 : G ∧¬G ⇔False
(11) 排中律: E19 : G ∨¬G ⇔1
(12) 等价式: E20 : G ↔⇔(G →H) ∧(H →G)
(13) 蕴含式: E21 : G →H ⇔¬G ∨H
(14) 假言易位: E22 : G →H ⇔¬H →¬G
(15) 等价否定形式: E23 : G ↔H ⇔¬G ↔¬H
(16) 归谬论: E24 : (G →H) ∧(G →¬H) ⇔¬G
这些为什么有用呢? 考虑有一天你在求解一个数学问题, 其中你想把一个命题否定掉, 比如
其中一个很重要的手段就是通过上面的这些重言式的替换. 就像在学习三角函数的时候使用三角恒等式替换一样.
下面我们来看一个比较有趣的逻辑代数推演的例子:
2.2.3. 我们已经知道 Bill, Jim和Sam分别来自Boston, Chicago和 Detroit. 以下每句话半句对, 半句错
能确定每个人究竟谁来自何处吗
先看前两个括号(上述式子红色的部分), 以连接两个式子中间的∧展开(下式红色符号), 我们有
根据已知条件, p1 ∧p4,p2 ∧p4,p1 ∧p3均为假的, 所以上述式子是
与后面的((p5 ∧¬p6) ∨(¬p5 ∧p6))进行∧操作, 也就是有
所以我们知道: p2,p3,p6是对的. #
事实上, 我们能这样做是因为有带入定理帮助我们.
𝔹onus
缺失的证明: 为什么没有了定理的证明?
一个很重要的问题是我们数学的基石是缺失的. 其实, 人类在认识世界的时候开始也是缺乏基础的, 仅仅凭借直觉来建立一些体系. 直到直觉无法完全覆盖的时候, 人类才开始探索有没有什么基础的支撑点来支持这一系列理论.
范式的意思是“规范的形式”. 那么, 这些内容化简到最后有没有一个目标呢? 其实是有的. 任何一个命题都可以写成“合取范式(CNF)”或者“析取范式(DNF)”的形式. 下面给出形如这样的式子的定义:
2.2.12 (合取范式 (Conjunctive Normal Form)). 我们称公式 α 是合取范式, 如果它形如
其中, 每个 βi 都形如
并且 βij 或是一个命题符号, 或者命题符号的否定.
2.2.13 (析取范式 (Disjunctive Normal Form)). 我们称公式 α 是析取范式, 如果它形如
其中, 每个 βi 都形如
并且 βij 或是一个命题符号, 或者命题符号的否定.
2.2.3. 每一个命题都有等价的合取范式和析取范式的形式. (Given any proposition, there exists a proposition in disjunctive normal form which is equivalent to that proposition.)
𝔻ialogue
A: 你真的想要看证明吗?
B: 嗯... 有点好奇.
A: 好, 给你看看. 不过有一些集合论的内容, 我们会在后面会讲解.
. (Copied from https://planetmath.org/everypropositionisequivalenttoapropositionindnf ) Any two propositions are equivalent if and only if they determine the same truth function. Therefore, if one can exhibit a mapping which assigns to a given truth function a proposition in disjunctive normal form such that the truth function f of this proposition is f, the theorem follows immediately.
Let n denote the number of arguments f takes. Define
For every X ∈{T,F}, define Li(x) = {T,F}n →{T,F} as follows:
Then, we claim that
On the one hand, suppose that f(Y ) = T for a certain Y ∈{T,F}n, By definition of V (f), we have Y ∈V (f). By definition of Li, we have
In either case, Li(Y )(Y ) = T, since a conjunction equals T if each term of the conjunction equals T, it follows that∨ i=1nL i(Y )(Y ) = T, Finally, since a disjunction equals T if and only if there exists a term which equals T, it follows the right hand side equals equals T when the left-hand side equals T.
On the one hand, suppose that V (Y ) + F for a certain Y ∈{T,F}. Let X be any element
of V (f). Since Y V (f), there must exist an index i such that Xi≠Y i. For this choice of i,
Y i = ¬Xi, Then we have
In either case,Li(X)(Y ) = F, Since a conjunction equals F if and only if there exists a term which evaluates to F, it follows that ∨ i=1n = F for all X ∈V (f). Since a disjunction equals if and only if each term of the conjunction equals F, it follows that the right hand side equals equals Fwhen the left-hand side equals F. □
𝔻ialogue
B: 看不懂的证明还有意义吗?
A: 这是一个很好的问题. 看似看不懂, 但是你在阅读的过程中会无意间记住一些话语, 那么将来你碰见相似的东西的时候, 就会感到快乐, 大多数情况下就更容易理解了.
B: 感觉我没办法一步到位诶...
A: 是的, 我们认识世界也是这样的, 一步一步的向前推进. 我们可以先有一个直观的印象, 慢慢做更加详细的探讨.
上面的只是给了我们一个正确性证明, 但是并没有告诉我们如何把一个式子化为合取范式或者析取范式. 一般的, 我们有如下的方法:
(1)用¬,∧,∨代替→,↔;
(2)用双重否定律, 消去律去掉多余的否定连接词, 运用De Morgan律将否定连接词内移.
(3) 利用分配率, 结合律, 幂等律整理得到.
实际上, 在上面的三个人从哪里来的例子中, 我们就用到了这样的想法.
𝔹onus
为什么合取范式(外面∧里面∨)和析取范式(外面∨里面∧)这么重要?
下面的这个回答来源于StackExchange上面的回答[?], 简要概括如下:
逻辑公式中的变量输入可以以复杂的方式混在一起. 如果公式采用CNF或DNF变量就更加分离从而更容易看出表达式何时成立. 比如, 要检查CNF是否成立只需逐个检查每个子句有一个是假的整个都是假的. DNF也类似: 逐个检查子句并在找到一个为真的子句时停止, 整个句子都是真的.
很多时候真值表会带来很多的麻烦: 意味着穷举和非常麻烦的事情. 有了CNF与DNF以后, 我们不必从真值表开始枚举, 可以通过操作表达式来形式地构造标准形式. 在某些情况下可能可以更方便一些.
下面我们来看一看合取范式与析取范式的一些性质.
我们发现, 在合取范式中, 只要有一个条件是假的, 那么整个命题都是假的. 在析取范式中, 只要有一个条件是真的, 那么这个命题是真的. 特别地, 如果每个命题变元或其否定恰好只有一个出现过并且只出现了一次, 那么我们说这个合取范式为极小项(析取范式为极大项). 比如我们有两个变量, 那么就可以有如下的四个逻辑表达式:
这样就保证了我们除了枚举输入的命题之外, 我们还可以枚举极小项, 极大项, 从两方面来观察命题的真假. 比如. 还是上面的两个命题符号的情形, 对于合取范式和析取范式, 分别有表2.2.3 以及表2.2.3的情形.
| P Q | ¬P ∧¬Q | ¬P ∧Q | P ∧¬Q | P ∧Q |
| 0 0 | 1 | 0 | 0 | 0 |
| 0 1 | 0 | 1 | 0 | 0 |
| 1 0 | 0 | 0 | 1 | 0 |
| 1 1 | 0 | 0 | 0 | 1 |
| P Q | ¬P ∧¬Q | ¬P ∧Q | P ∧¬Q | P ∧Q |
| 0 0 | 0 | 1 | 1 | 1 |
| 0 1 | 1 | 0 | 1 | 1 |
| 1 0 | 1 | 1 | 0 | 1 |
| 1 1 | 1 | 1 | 1 | 0 |
𝔹onus
列表有什么好处? 我们可以发现什么规律?
我们发现每一个赋值对应一个取值为的极
项, 每个极
项的
赋值是唯一的. 并且没有等价的两个极
项, 任何两个不同的极
项
取必为真, 极
的否定是极
,
所有的极
项的
取为永假公式.
𝔻ialogue
A: 这个和二进制表示好像. 我们能不能有一种方法来用一个整数来表示命题?
B: 确实, 但是需要考虑一下命题变元的记号问题.
如果我们把合取范式和析取范式里面的内容都变为极小项/极大项的时候, 我们就可以得到更标准, 更易于处理的内容. 通常称为主合(析)取范式.
2.1_____________________________________________________________________________
符号化下列命题:
vii. 1 is the factorial of 0, and u is the factorial of x+1 if v is the factorial of x and u is v times.
设 P: 数理逻辑很有趣; Q: 作业很难; R: 这门课程使人喜欢. 将下列句子符号化:
构造如下命题公式真值表并判断其类型:
我们发现, 蕴含词的逻辑永真式和我们经常所做的推理有很好的联系. 具体地, 如果α →β, 那么如果α成立, 可以推导出β为真.
同样的, 如果假设α成立, 只要经过合理的推导可以推导出β为真, 那么这个规则就是成立的.
我们在推理时多半用“因为...所以...”, 那么前面的什么概念能起关键作用呢?
一般而言, 逻辑推理有一系列的假设前提A1,A2,,An, 有一个结论B, 什么是正确的推理呢? 形式化地, 对前提与结论所涉及的逻辑变量任意赋值,
如果任意的Ai均为这真, 它们的合取式的值当然也为真, 那么B必为真.
形式化的, 我们就说: 这样的推理是正确的.
2.3.1. 设G1,G2,,Gn,H是命题公式, 对任意指派I, 如果G1∧G2∧
∧Gn为真, H也为真, 或者G1∧G2∧
∧Gn为真,
H为假, 那么称H是G1,G2,
,Gn的逻辑结果. 或者G1,G2,
,Gn共同蕴含H, 记做G1 ∧G2 ∧
∧Gn ⇒H.
需要注意的是, ⇒是一个关系, 这是一个不可计算的公式.
2.3.2. 设G1,G2,,Gn,H是命题公式, 如果H是G1,G2,
,Gn的逻辑结果,
那么称G1,G2,
,Gn ⇒H是有效的或正确的. 否则称为无效的.
称G1,G2,,Gn为一组前提, H为结论, 如果记Γ = {G1,G2,
,G3}, 上述关系可以记作Γ ⇒H.
𝔻ialogue
A: 如果我有一个有效的推理, 那么结论应该是正确的吧?
B: 那可不一定. 举个例子: 1 + 1 = 3,2 + 2 = 4 ⇒114 + 514 = 191虽然形式是有效的, 但是结论确实是不对的.
A: 确实, 很像是→记号的拓展. 如果前提条件为假, 那么就不关心结论的正确性了.
所以这就解释了我们为什么经常使用的因为...所以...是合理的了. 比如(p ∧(p ∧q)) →q是永真的, 那么就可以有三段论这样的合理的推理过程了.
𝔼xample:
一个三段论的示例如下:
关爱学生, 好好讲课, 有真才实学的老师会被学生欢迎
朱富海老师关爱学生, 好好讲课, 有真才实学
朱富海老师受学生欢迎.
我们经常对于知识研究一些规律. 比如在逻辑公式很长的时候, 逐个枚举是十分低效率的. 比如, 如果有200个命题符号的逻辑公式, 用计算机枚举则需要2200种情况. 用Python的强大的计算器可以知道, 需要核验的情况是一个61位数.
𝔼xample:
我们可以使用ipython中输入len(str(2**200))知道它的位数. Python自带高精度计算, 因此如果直接输入2**200, 它就会直接把数字算出来!
既然要推理, 我们就要有推理的定律和推理的推理的规则. 正如前面说的程序语言的语法和语义类似.
经过总结归纳, 我们有如下的推理定律:
2.3.2 (常见的推理定律). 设G,H,I,J是任意的命题公式, 那么我们有:
(1) 简化规则: I1 : G ∧H ⇒G, I2 : G ∧H ⇒H.
(2) 添加规则: I3 : G ⇒G ∨H, I4 : H ⇒G ∧H.
(3) I5 : G,H ⇒G ∧H.
(4) 选言三段论: I6 : ¬G,G ∨H ⇒H.
(5) 分离规则: I7 : G,G →H ⇒H.
(6) 否定结论: I8 : ¬H,G →H ⇒¬G.
(7) 连续推理: I9 : G →H,H →I ⇒G →I.
(8) 两难推理: I10 : G ∨H,G →I,H →I ⇒I
一个学习的很好的方法是举一些例子. 我们可以用上面的符号翻译成具体的例子. 不用太过于拘束.
𝕀dea
遇见新概念的时候, 可以应该举一些例子辅助理解, 尽可能弄懂来龙去脉.
以最后一个例子为例, 有:
𝔼xample:
𝔹onus
为什么叫他们为基础的规则? 是不是因为他们具有某种完备性?
推理规则可以使用真值表验证. 除此之外, 我们还需要推理定律: 也就是需要完成什么样的变换. 我们有三条规则.
(1) Premise规则: 前提引用. 如果推理的时候引入了前提集合中的一个前提, 那么称为使用了P规则;
(2) Transformation规则: 逻辑结果引用的规则. 在推理过程中, 如果引入推理过程中某个产生的中间结果, 那么称使用了T规则;
(3) Conclusion premise规则: 附加前提规则. 在推理过程中, 如果逻辑结果为一个含有蕴含→的式子, 那么把它的前提条件作为假设引入, 就是用了CP规则. 所有引入的假设最终必须被“释放” (discharged) 所谓释放, 其实就是在使用假设α作为假设的前提下推出了β, 最后要写成α →β的形式. 这就是假设的释放.
我们来推导一下I6.
. (1) 直接引入前提集合的前提, 有¬G;
(2) 直接引入前提集合的前提, 有G ∧H;
(3) 使用(1),(2)的中间结果, 有¬G ∧(G ∨H);
(4) 使用(3)的中间结果, 使用分配律,有(¬G ∧G) ∨(¬G ∧H);
(5) 使用(4) 的中间结果, 有¬G ∧H;
(6) 使用(5)的中间结果, 有H. □
对于I9, 我们可以先把G是对的引入集合, 然后最后推理得到I的时候, 为了说明它的正确性, 就需要使用CP规则.
𝔹onus
P规则和T规则能足够做所有的内容的推理吗?
在上面我们做的研究中, 我们会发现很多东西相当的机械化. 于是, 在有机械化的内容出现的时候, 计算机就有用了. 所以, 我们希望找到一种方法, 使得计算机可以自动地推理我们的命题. 在1965年, J.A. Robinson发现了消解原理: 它的原理是规则I7. 具体的有:
2.3.3 (消解与消解式). 设G和H是两个析取式, 如果G中有变元P,H中有变元¬P, 则从G和H中分别消去P和¬P, 并且将余下的部分析取, 构成新的表达式W, 这个过程称为消解. W为G,H的消解式.
我们经过消解的方法, 立即可以得到一个很有“自动化”意思的定理:
2.2_____________________________________________________________________________
请写一个Python程序, 输入一个命题公式(形式自己指定), 输出一个填写好的真值表的填写(形式同样自己指定). 提示: 一开始不要搞得太复杂. 比如只接受五个逻辑连接词的某两个, 然后慢慢扩展.
请写出一个Python程序, 使得我们可以把一个命题问题化为合取范式.
经过我们前面的一些探索, 我们就有资本忘记以前学过的所有的东西了. 现在, 让我们来形式化这一切–用公理和原则来进行推演. 以前的内容带来的直觉会对我们在形式系统里面操作产生引导的作用. 下面我们来看一些规则:
如下是若干个可以完成任何规则的: 其中像分数线一样的上方表示的是前提, 下方表示的是结论. 有时候我们可以把它写成一行就成了{前提}⊢结论.
我们只用上面的一些内容就可以得到更加复杂的推理规则: 比如我们有前提A →B,¬A →A, 尝试推出结论B. 我们可以用上面的推理规则这样推理:
𝔻ialogue
A: 其实还是知道如何分类讨论就行了... 看看它的假设也是很明确的.
B: 确实. 我们能从这里得到哪些更多的东西呢?
我们发现命题逻辑无法表达部分与整体的关系. 例如:
𝔼xample:
(1) 张三是个法外狂徒;
(2) 李四与张三是好朋友;
(3) 李四也是一个法外狂徒;
(4) 王五站在张三与李四中间;a a王五害怕极了...
(5) 王五长得比张三与李四都高;
(6) 所有的法外狂徒终将绳之以法;
(7) 存在法外狂徒改过自新.
我们发现以前学过的东西仅仅能应对很基本的内容. 比如任意, 存在无法表示. 下面我们形式化的先来说说什么是任意和存在. 这些是对于一类类似于变元的内容的性质的总体描述. 因此, 我们首先定义什么是谓词
2.5.1 (谓词(predicate)). 在不能被拆分为更小的命题中(通常叫做原子命题(automic expression)), 可以独立存在的客体(subject)(通常是句子中的主语, 宾语)称为个体词(individual), 描述客体的性质或客体之间的关系的部分称为谓词.
很多时候, 我们会泛指一些很笼统的概念, 比如“人”. 也有时候我们会举一些明确的个体, 比如“蒋炎岩老师(图2.3)”. 这时候我们就需要区分“个体变量”(通常是泛指)和“个体常量”(通常是特指).

2.5.2 (个体常量, 个体变量, 个体域, 全总个体域). 对于具体明确的个体而言, 称为个体常量(individual constant), 一般用形如a,b,a1,b1这样的小写字母表示. 个体变量(individual variable)取值范围称作个体域(或论域, individual field), 通常用字母D表示. 我们通常把宇宙间所有个体聚集在一起的个体域称为全总论域(universual individual field).
2.5.3 (n元命题函数). 设P(x1,x2,,xn)是n元函数(function), 其中每一个变量可以取其可以取到的对应的值.
如果P的值域是{0,1}, 那么说P(x1,x2,
,xn)是n元命题函数或n元谓词(n-ary propositional function).
这样子, 我们就可以更加方便的定义量词(qualifier)了.
2.5.4 (全称量词与特称量词). 表达全部数量关系的词语诸如“一切”,“所有”,“每一个”等称为全称量词(universal quantifier), 记作∀. 如所有的x记作∀x.
表达部分数量关系的词语诸如“存在”, “有一个”, “有一些”称为存在量词(existential quantifier). 记作∃. 如有一些x记作∃x.
这里面, x被称为作用变量(function variable), 一般将量词加在对应的谓词之前, 如∀x.F(x)或∃x.F(x). 此时F(x)被称为全称量词和存在量词的作用域(又成为辖域, scope).
上面的内容一个很重要的地方在于引入了变元. 例如, 在函数符号和谓词符号中, 变元的引入使得我们要讨论的事情变得更加多了.
𝔹onus
你在哪里还见到过由常数引入到变量? 其实, 我们在初中的时候, 先研究了二次方程的解, 再把x当做一个变元, 研究所有x构成的二元组(x,f(x))的一些性质. 有兴趣学习高等代数的同学会发现在引入λ −矩阵的时候也用了这样的知识.
这下子, 我们就可以定义谓词逻辑的构成了.
2.5.5 (谓词逻辑的构成). 谓词逻辑由且仅有以下的几部分构成:
(1)逻辑联词: ¬,∧,∨,→,↔
(2)量词符号: ∀ (forall; 全称量词), ∃ exists; 存在量词)
(3)变元符号: x,y,z,…
(4)左右括号: (,)
(5)常数符号: 零个或多个常数符号 a,b,c,…, 表达特殊的个体
(6)函数符号: n-元函数符号 f,g,h,… (n ∈ℕ+), 表达个体上的运算
(7)谓词符号: n-元谓词符号 P,Q,R,… (n ∈ℕ), 表达个体的性质与关系
和普通公式一样, 谓词公式也是由一项一项构成的.
2.5.7 (公式 (Formula)). 谓词逻辑的公式定义如下:
我们来举一些例子:
𝔼xample:
0 不是任何自然数的后继
两个自然数相等当且仅当它们的后继相等
x 是素数 (x > 1 且 x 没有除自身和1之外的因子)
哥德巴赫猜想 (任一大于2的偶数, 都可表示成两个素数之和)
| ∀x. (SS0 < 2 ∧(∃y. 2 ×y = x)) → | |||
| (∃x1. ∃x2. Prime(x1) ∧ Prime(x2) ∧x1 + x2 = x) |
有了坐标系, 辩证法进入了数学. 有了坐标系, 运动进入了数学. –Engels
这里的“运动”, “坐标系”只是变量引入数学的结果. 自然, 这让我们探索的内容更加的丰富, 同时也更加容易犯错了. 比如, 我们很多时候喜欢对变量做替换. 但是, 下面的代换显然是错的:
𝔼xample:
“那曲市” := “中国最大的城市”
“那曲市”有三个汉字
“中国最大的城市”有三个汉字
因为“中国最大的城市”这个字符串有7个汉字构成. 这就警告我们要在变量代换的时候要格外小心. 那么, 变量有哪些类型呢?
在公式∀x.P(x,y) ∨∃y.R(x,y)中, 根据量词作用域的定义, ∀x的作用域是P(x,y), 因此x受到了∀x的约束, 从而把这个变元称作约束变元. 然而这个的y没有受到∀x的约束, 所以称为自由变元.
2.5.8 (约束变元与自由变元). 给定公式∀x.G和∃x.G, G为∀x和∃x的作用域, 那么G中的x出现的都是约束出现(bounded occurrence), 称变元x则是约束变元(bound variable), G中不同于x的其他变元出现的则是自由出现(free occurrence), 称这些变元为自由变元(free variable)
𝔻ialogue
A: 这就像C语言里面判断一个变量是不是被定义过了一样! 如果被定义过了, 自然不能乱搞, 如果没有定义过, 改个和定义过的名字不一样的, 应该也是等价的.
B: 对, 名字是次要的, 真正的表达的东西才是核心啊!
可能由于重名的原因, 我们发现同样一个字母既可以表示自由变元, 又可以表示约束变元, 这样就很不利于我们问题的分析. 为此, 我们给出变元的代换规则, 可以让每一个符号各司其职.
对变元可以做如下的变量替换, 推理是有效的:
(1) 约束变元改名. 将量词作用域内与作用变元相同的约束变元用新的个体变元替换. 新的变元要与作用域的其他变量名符号不同.
(2) 自由变元带入. 将公式中的某个自由变元的每一处用新的个体变元或个体常量带入. 并且新变元不允许在公式中以任何约束形式出现.
上面的两条关系在带入之前和带入之后都没有改变原有命题之间的约束关系. 但是使用(2)之后, 公式的含义就发生了变化, 但是推理是成立的–比如选择常量带入进去, 那么命题就退化成了一个特化的情况了.
没有自由变量的公式有着很好的性质–他的真值表就可以确定了. 我们把这样的内容叫做闭式.
在命题逻辑中, 我们运用了真值指派的方式来了解了这个命题的真值情况, 那么这里, 我们能不能也用类似的方法“解释”一个命题逻辑的含义呢?
谓词公式的解释远远没有我们想象的那么简单! 在不同的数学结构中, 同一个谓词公式很可能有不同的结果!
𝔼xample:
考虑
α 在数学结构𝒰= ℚ中是真的, 但是在数学结构𝒰= ℝ中是假的.
从上面的例子, 我们可以看出来, 要想解释清楚一个谓词逻辑的公式, 我们需要考虑对象所处的数学空间来下结论. 也就是一个表达式的语义大致取决于:
也就是这种“解释”将公式映射到一个数学结构 𝒰上, 这决定了该公式的语义.
什么是解释呢? 更正式一点, 我们认为一个公式的解释由下列四部分组成:
2.6.1. 谓词逻辑中的谓词公式G的一个解释(interpretation)I由以下的四部分构成:
(1) 非空的个体域D;
(2) G中的每个常量符号, 指定D中的某个特定的元素.
(3) G中的每个n元函数符号, 指定的是每一个元随意选择得到的所有可能的结果的集合对应到D的一个函数
(4) G中的每个n元谓词符号, 指定每一个元随意选择得到的所有可能的结果的集合到{0,1}的某个特定的谓词.
因此, 我们给出在一个特定的数学结构上“满足”的定义.
同样的, 我们也可以说明语义蕴含在谓词逻辑中的定义:
当然, 我们当然希望为公式能够在等价的意义下能够完成推理. 所以我们需要首先研究什么样的公式在怎样的情形下是等价的.
| E25 : ∀x.G(x) ⇔∀y.G(y) | ||
| E26 : ∀x.G(x) ⇔∀y.G(y) |
(2) 量词转换率/量词否定等值式(对偶原理):
| E27 : ¬∃.G(x) ⇔∀x.¬G(x) | ||
| E28 : ¬∀.G(x) ⇔∃x.¬G(x) |
(3) 量词作用域的扩展/收缩:
| E29 : ∀x.(G(x) ∨S) ⇔∀x.G(x) ∨S; | ||
| E30 : ∀x.(G(x) ∧S) ⇔∀x.G(x) ∧S; | ||
| E31 : ∃x.(G(x) ∨S) ⇔∃x.G(x) ∨S; | ||
| E32 : ∃x.(G(x) ∧S) ⇔∃x.G(x) ∧S; |
(4) 量词的换序:
| E33 : ∀x.G(x) ∨∀x.H(x) ⇔∀x∀y.(G(x) ∨H(y)) | ||
| E34 : ∃x.G(x) ∧∃x.H(x) ⇔∃x∃y.(G(x) ∧H(y)) |
(5) 量词分配率:
| E35 : ∀x.(G(x) ∨H(x)) ⇔∀x.G(x) ∨∀x.H(x) | ||
| E36 : ∃x.(G(x) ∧H(x)) ⇔∃x.G(x) ∧∀x.H(x) |
(6) 对于多个量词的命题公式, 若G(x,y)是含有自由变量y的谓词公式, 那么有
| E37 : ∀x∀y.G(x,y) ⇔∀y∀x.G(x,y) | ||
| E38 : ∃x∃y.G(x,y) ⇔∃y∃x.G(x,y) |
注意到全称量词对于合取式子是可以分配的, 存在量词对于析取式子是可以分配的. 我们有时候是可以通过这个来简化计算.
仿照命题公式, 我们也想看一看, 谓词公式最后有没有一个统一的形式, 使得我们的表达和交流更加的方便.
当然, 命题逻辑公式有与之等值的范式. 谓词逻辑公式也有范式, 但不是所有范式都与原公式等值, 有一些可能条件会相对弱化一些, 下面介绍两个形式.
我们想, 任何的内容是不是都可以把所有的量词提到前面, 后面的内容就没有量词记号了. 这就会给我们的证明和讨论带来很好的方法.
那么这个内容是不是存在的呢? 是不是唯一的呢? 实际上, 这是存在的, 但是不是唯一的.
𝔻ialogue
A: 我还是希望看一下证明.
B: 好的. 这部分的证明可以在《Classical mathematical logic : the semantic foundations of logic》这本书里面找到, 下面抄一下里面的证明.
. (Copied from Page 108: Normal form theorem) We proceed by induction on the length of A to show that first A has a prenex normal form. If A is atomic or is quantifier free, we are done. So suppose theorem is true for all wffs(Well-formed formula, finite sequence of symbols from a given alphabet that is part of a formal language) shorter than A.
Suppose A has the form ¬C. Then by induction there is a wff C∗ in prenex normal form for C. By Corollary 11, we are then done.
Suppose A has the form C ∧ D, Then by induction C and D have prenex normal
forms, Q1y1QnynC∗ and Qn+1z1
Qn+mymD∗. By Theorem 3 we can substitute so
that we may assume that no yi is a zi. Then by parts (e)–(h) of the Tarski-Kuratowski
algorithm,Q1y1
QnynQn+1z1
Qn+mzmC ∗∧D∗ is semantically equivalent C ∧D, and is in
prenex form,and satisfies (ii) and (iv). The case when A has the form C ∧D is done similarly.
Suppose that A is of the form C →D. Then C →D is semantically equivalent in PC to ¬(C ∧¬D). So we can use Theorem 7 and what we’ve already established.
If A has form ∀C. then by induction there is a wff C∗, in prenex normal form for C.Hence, by Theorem 1, Theorem 4, and Theorem IV.4, we are done. If A is of the form ∃x.C the proof is the same.
Finally, by applying Theorem 7 and the normal form theorem for propositional logic to a prenex normal form for A, we can obtain both a conjunctive normal form for A and a disjunctive normal form for A. □
𝔻ialogue
B: 呃呃. 怎么还引用起来了其他的定理了啊...
A: 这可是一本书里面的一个部分. 所以说这一章的名字叫简单的数理逻辑.
我们发现, 前束范式虽然能够把两次放在最前端, 但是不唯一.
要想唯一, 就要牺牲一点“等价性”. 这个意思就是说得到一个比原来命题结果要弱一些的结果. 这样, 我们就可以得到Skolem范式.
是一个前束合取范式, 按照从左往右的顺序去掉G中存在的量词, 若Qi是存在量词, 且i = 1, 则直接用个体常量代替M中的所有的x1, 并且在G中删除Q1x1.
若i > 1,Q1,Q2,,Qi−1都是全称量词, 则在G中使用一个未使用过的函数符号, 如f, 并且用f(x1,x2,
,xi−1)替换G中的所有的xi,
然后删去Qixi. 重复这个过程, 直到G中没有量词为止.
𝔼xample:
求
的Skolem范式.
| ⇔¬(¬∀x∃yP(x,y) ∨∃x(¬¬∀yQ(y,a) ∨R(b,x))) | |||
| ⇔∀x∃yP(x,y) ∧¬∃x(∀yQ(y,a) ∨R(b,x)) | |||
| ⇔∀x∃yP(x,y) ∧∀x(∃y¬Q(y,a) ∧¬R(b,x)) | |||
| ⇔∀x(∃yP(x,y) ∧∃y¬Q(y,a) ∧¬R(b,x)) | |||
| ⇔∀x(∃yP(x,y) ∧∃z¬Q(z,a) ∧¬R(b,x)) | |||
| ⇔∀x∃y∃z(P(x,y) ∧¬Q(z,a) ∧¬R(b,x)) |
现在消去存在y, 有
然后消去存在z, 有
#
相比于命题逻辑, 谓词逻辑要求的内容就多了不少了. 具体的, 我们可以把全称量词, 特称量词替换掉. 或者把它们替换掉为一个特殊的命题. 这样我们就可以把谓词逻辑转化为谓词逻辑了. 因此, 我们有如下的简化的一节逻辑的推理原则.
2.8.1 (“任意”符号消去). ∀-eliminating.
where α is free for x in α.
The symbol α[t∕x] means substituting all the occurrences t in α to x.
2.8.2 (“任意”符号的引入). ∀-introducing.
| [t] | 引入变量t | |||||
| 经过一系列推理 | ||||||
| α[t∕x] | 得到的表达式所有的x都是t | |||||
| ⊢∀x.α | 就可以推出任意了 |
where α is free for x in α.
The symbol α[t∕x] means substituting all the occurrences t in α to x.
下面我们来举一个例子来看看:
𝔼xample:
{P(t),∀x(P(x) →¬Q(x)}⊢¬Q(t)
| P(t) | P | |||||
| ∀x(P(x) →¬Q(x)) | P | |||||
| P(t) →¬Q(t) | Universal Specification | |||||
| ¬Q(t) | T |
#
我们再来看一个例子:
𝔼xample:
{∀x(P(x) →Q(x)),∀x.P(x)}⊢∀x.Q(x)
解答如下:
| ∀x.(P(x) →Q(x)) | (P) | |||||
| ∀x.P(x) | (P) | |||||
| (引人变量 ) | ||||||
| P | (∀-elim ,(1),(3)) | |||||
| P | (∀-elim, ,(2),(3)) | |||||
| Q | (→ -elim ,(4),(5)) | |||||
| ∀x.Q(x) | (∀-intro ,(3) −(6)) |
#
上面我们介绍了如何把含有任意的内容干掉或者引入. 下面我们来看一下关于存在的一些例子:
这个定理的意思是: 如果α对于某个项成立, 那么∃x.α 成立.
这里的没有被约束, 我们来举一个例子: P(c) ⊢ ∃x.P(x),c是任意的常元符号: 这样是可以的, 但是注意下面的例子: ∀y.(y = y)⊬∃x.∀y.(x = y)(y is not free for x in α)
存在符号也可以消去. 第一种方式就是上面的反方向的形式. 就是
还有一种我们以前经常用到的方法. 我们在这里来看一下, 这也是存在量词消去的一种方法.
这个内容说的是什么呢? 考虑我们在高中做题的时候, 对于存在性问题, 我们一般是假设这个存在, 经过一系列推导之后发现确实存在, 于是就说明了这个东西确实是存在的. 更加形式化的就是: 假设x0使得α成立, 如果从α[x0∕x]可以推导出β, 那么α从可以推导出β.
我们来看个简单的例子:
𝔼xample:
{∀x.(P(x) →Q(x)),∃x.P(x)}⊢∃x.Q(x)
| ∀x.(P(x) →Q(x)) | ( 前提 ) | |||||
| ∃x.P(x) | (前提 ) | |||||
| ( 引入变量与假设 ) | ||||||
| P | (∀-elim, (1),(3)) | |||||
| Q | (→ -elim, (3),(4)) | |||||
| ∃x.Q(x) | (∃-intro ,(5)) | |||||
| ∃x.Q(x) | (∃-elim, (2),(3) −(6)) |
#
𝔼xample:
{∃x.P(x),∀x.∀y.(P(x) →Q(y)}⊢∀y.Q(y)
| ∃x.P(x) | ( 前提 ) | |||||
| ∀x.∀y.(P(x) →Q(y)) | ( 前提 ) | |||||
| ( 引入变量与假设 ) | ||||||
| ∀y. | (∀-elim, (2),(3)) | |||||
| ( 引入变量 ) | ||||||
| P | (∀-elim, (4), (5)) | |||||
| Q | (→ -elim, (3),(6)) | |||||
| Q | (∃-elim, (1), (3) −(7)) | |||||
| ∀y.Q(y) | (∀-intro, (5) −(8)) |
#
上一次我们说到了因为(p ∧(p →q)) →q是永真式, 因此我们有了(p ∧(p →q)) ⇒q. 三段论的内容被叫做Modus Ponens.
Modus Ponens来源于古拉丁文, 翻译成英语就是 method of putting by placing. 也就是说, 在推理的过程中, 如果p是真的, p →q, 那么q是可以被接受的.
为什么呢? 因为如果有含蕴含词的永真式(A1 ∧A2 ∧∧An) →B, 利用推理规则, 我们就能从前提条件A1 ∧A2 ∧
∧An推出B,
以及A1 →(A2 →... →(Ak →B)
𝔹onus
蕴含记号支持结合律吗? 支持交换律吗?
在中学, 我们学习了充分条件, 必要条件, 以及四种命题.
𝔻ialogue
A: 现在我知道如何否定命题“若p则q”了!
B: 很好! 注意一下四种命题. 为什么命题和它的逆否命题真假性是一致的?
先对充要条件做描述: 充要条件是(P →Q) ∧(Q →P) →(P ↔Q)
比如来看下面的问题:
充分条件很容易说明. 但是必要条件如何说明呢? 我们高中知道命题和逆否命题真假一致, 能从命题逻辑的角度说明吗?
其实很容易. (P →Q) ↔(¬Q →¬P)是永真式就行了. 我们就有更加公理化的方法完成了证明.
我们发现结论是析取式子(或), 那么我们应该如何证明? 我们考察永真式(P ∧Q) ↔(¬P ∧Q);(P ∧Q),¬P ⇒Q. 为之构造一个合理的语言描述, 然后翻译成符号语言看上去是很好的一个方法.
Hardy说证明是无理数是最漂亮的证明之一. 其中用了反证法. 不妨自己写出一个证明.
𝔻ialogue
A: 我感觉好难...
B: 那是因为高中没有学过数论! 去了解一些基本的整数的性质吧! 很多时候感觉困难只是因为前置知识没有做好. 补充上去就行了.
反证法之所以能成立, 是因为¬A ⇒C, ¬A ⇒¬C, 必然有C ∧C ⇒False. 根据上述的内容, (p →q) ∧(¬q)) →¬p, 所以化简得到¬¬A = A.
𝔹onus
我们应该如何否定含有量词的命题? 留到下一章节.
在分牌的时候, 我们可以使用这个小魔术:
(1) 将一副纸牌按照红黑相间的模式排好;
(2) 按照传统方式洗一次牌, 分牌时两叠牌显出的两张颜色互异;
(3) 你能做到将牌放在背后(自己看不见), 却能保证每次抽出两张牌, 始终是一红一黑吗?
这个过程的证明可以使用数学归纳法描述. 回忆一下数学归纳法的常见过程. (1) 归纳奠基; (2) 归纳假设; (3)结论.
我们现在进行一个灵魂拷问:
𝔹onus
为什么数学归纳法在逻辑上是正确的?
事实上, 其合理性来自证明对象结构的定义.
2.9.1 (Peano 公理). 自然数的Peano公理有如下几条:
对于自然数的归纳正确性, 我们还需要良序原理(well-ordering principle). 可能需要很多的背景知识, 在这里仅仅给出基本的定义.
2.9.1 (第一数学归纳法 (The First Mathematical Induction)). 设 P(n) 是关于自然数的一个性质. 如果
那么, P(n) 对所有自然数 n 都成立.
除了第一类数学归纳法, 其实还有更加强大的第二类数学归纳法. 并且两者之间是等价的.
2.9.2 (第二数学归纳法 (The Second Mathematical Induction)). 设 Q(n) 是关于自然数的一个性质. 如果
那么, Q(n) 对所有自然数 n 都成立.
我们可以来证明这两者是互相蕴含的. 当然这个证明的关键是性质选取的任意性. 我们可以用这个来让它对我们有利.
第二数学归纳法也被称为“强” (Strong) 数学归纳法, 它强在可以使用的条件更多了. 我们可以来证明这件事情.
. 要证第二类数学归纳法也即任给一个命题 F 若满足 F(1) 及 (F(1) ∧F(2) ∧∧F(n)) ⇒F(n + 1) 则有 ∀k ∈ℕ.F(k)
. 那么我们可以构造命题 G(n) := F(1) ∧F(2) ∧
∧F(n) . 显然 G(n) ⇒ F(n + 1) 又有 G(n) ⇒ G(n) 则
G(n) ⇒(F(n + 1) ∧G(n)) 而 后者即为 G(n + 1) . 故命题 G 满足第一类数学归纳法的条件所以 ∀k ∈ℕ . G(k) 成立. 而
G(k) ⇒F(k) 故 ∀k ∈ℕ . F(k) 也即第二类数学归纳法成立. □
. 要证第一类数学归纳法也即任给一个命题 F 若满足 F(1) 及 F(n) → F(n + 1) 则有 ∀k ∈ ℕ . F(k) . 显然 F 是满足第二类数学归纳法的条件的 (因为 1 的条件比 2 强)故根据第二类数学归纳法 F(k) 对所有正整数 k 成立也即第一类数学归纳法成立. □
𝔻ialogue
A: 数学归纳法这么好, 感觉什么整数的问题都能证明啊!
B: 其实没有你想象的那么简单. 《具体数学》上有关于它的论述, 但是我一时间找不到了.
最后, 我们用一个例子来结束这一节. 这是一个很烧脑的问题, 据说是由Terry Tao放在他的个人主页上的一道题.
2.9.4. Of the 1000 islanders, it turns out that 100 of them have blue eyes and 900 of them have brown eyes, although the islanders are not initially aware of these statistics (each of them can of course only see 999 of the 1000 tribespeople).
One day, a blue-eyed foreigner visits to the island and wins the complete trust of the tribe.
One evening, he addresses the entire tribe to thank them for their hospitality.
However, not knowing the customs, the foreigner makes the mistake of mentioning eye color in his address, remarking “how unusual it is to see another blue-eyed person like myself in this region of the world”.
What effect, if anything, does this faux pas (失礼) have on the tribe?
答案比较令人出乎意料:
2.9.4. Suppose that the tribe had n > 0 blue-eyed people.
Then n days after the traveller’s address, all n blue-eyed people commit suicide.
. 考虑采用数学归纳法:
仔细考察这个例子, 考虑 n = 1,n = 2 的简单情况, 出现了类似“我知道你知道我知道 …”的思维递归情形. 数学归纳法帮我们挑选了其中的相邻两层, 让我们更加清楚的直面问题.
𝕀dea
考虑递归问题的时候, 在非边界条件的情形下, 只用考虑连续的两层就可以了. 关注状态变化.
𝔹onus
刚刚的魔术, 为什么不是关于自然数的, 也能用数学归纳法证明?
𝔹onus
为什么鸽巢原理叫做“原理”而不是“公理”, “定理”?
这里有一个数独.
1from z3 import * 2 3# First we create an Integer Variable for each cell of the Sudoku grid. 4# Each cell must contain a digit (1 to 9) 5X = [ [ Int("x_%s_%s" % (i+1, j+1)) for j in range(9) ] 6 for i in range(9) ] 7 8# Every digit has to be placed exactly once in each row 9cells_c = [ And(1 <= X[i][j], X[i][j] <= 9) 10 for i in range(9) for j in range(9) ] 11 12# Every digit has to be placed exactly once in each column 13rows_c = [ Distinct(X[i]) for i in range(9) ] 14 15cols_c = [ Distinct([ X[i][j] for i in range(9) ]) 16 for j in range(9) ] 17 18# Every digit has to be placed exactly once in each 3x3 subgrid 19sq_c = [ Distinct([ X[3*i0 + i][3*j0 + j] 20 for i in range(3) for j in range(3) ]) 21 for i0 in range(3) for j0 in range(3) ] 22 23sudoku_c = cells_c + rows_c + cols_c + sq_c 24 25instance = ((5,3,0,0,7,0,0,0,0), 26 (6,0,0,1,9,5,0,0,0), 27 (0,9,8,0,0,0,0,6,0), 28 (8,0,0,0,6,0,0,0,3), 29 (4,0,0,8,0,3,0,0,1), 30 (7,0,0,0,2,0,0,0,6), 31 (0,6,0,0,0,0,2,8,0), 32 (0,0,0,4,1,9,0,0,5), 33 (0,0,0,0,8,0,0,7,9)) 34 35# Note that we use the number 0 to indicate blank fields. We need to convert this input to the variables managed by z3: 36 37instance_c = [ If(instance[i][j] == 0, 38 True, 39 X[i][j] == instance[i][j]) 40 for i in range(9) for j in range(9) ] 41 42s = Solver() # (1) 43s.add(sudoku_c + instance_c) # (2) 44if s.check() == sat: # (3) 45 m = s.model() # (4) 46 r = [ [ m.evaluate(X[i][j]) for j in range(9) ] # (5) 47 for i in range(9) ] 48 print_matrix(r) # (6) 49else: 50 print("failed to solve") # (7)
我们在之前知道, 计算机解题的正确性在于正确算法的实现. 那么算法的正确性来源于什么呢? 不同于人类指令的有歧义和模糊, 机器语言应该做到的是有明确的“基本指令”, 与“控制结构”.
(对于初学者而言, ) 精确的定义毫无意义.(见图2.4) –蒋炎岩
无论如何, 先忘掉这些抽象的名词吧. 基本指令就可以想象成一行代码是如何进行的, 它是如何操作了计算机的内部的. 控制结构是一些描述那个当前的代码执行如何执行下一条指令的一系列规约. 也就是描述了基本算法是什么, 以及是如何被实施的.
生活中很多的事情都可以用一些控制结构完成. 我们来举几个例子:
𝔼xample:
吃一只蟹黄包的算法.
如何确保我们的过程无误? 其实我们可以在执行完之后进行监视. 每一个guard需要看一看前面的内容是不是已经完成了即可.
如果我们不打算只吃一只, 那么我们如何控制数量呢?
一个很有趣的问题是: 如何确定循环的过程是正确的? 我们可以发现, 虽然循环的变量在变, 但是我们总是希望维系一个命题的值是真的. 由此我们引入“循环不变式”.
例如, 我们使用累乘的方法去循环的时候, 循环不变式可以是“存放中间结果的量的值=a×循环变量当前的值.
类似于数学归纳法, 我们可以利用循环不变式证明循环算法证明的一个基本的方法:
2.10.1 (证明循环不变式的基本方法). (1) Initialization. It is true prior to the first iteration of the loop.
(2) Maintenance. If it is true before an iteration of the loop, it remains true before next iteration.
(3) Termination. The loop terminates, and when it terminates, the invariant – usually along with the reason that the loop terminated–gives us a useful property that helps show that the algorithm is correct.
下面我们为上述的两种吃蟹黄汤包的策略选定一个循环不变式. 对于策略I, 我们有在循环终止之前, 我还是没有饱的; 对于策略II, 我们的循环不变式是计数器的值=存放临时变量的值+1
我们发现不变量对于问题求解有很大的价值. 比如下面的这个问题:
答案是15场. 因为每一次循环满足不变量: 这一次的值=上一次的值-1. 由此就可以归纳了.
与之类似的问题,
2.10.3. A rectangular chocolate bar is divided into squares by horizontal and vertical grooves, in the usual way. It is to be cut into individual squares. A cut is made by choosing a piece and cutting along one of its groove. (Thus each cut splits one piece into two pieces) How many cuts are needed to completely cut the chocolate into all its squares?
解答的方法也是和前面的完全一样, 他们是遵循同一个“差1”的不变量的. 这就是不变量对于问题求解的价值.
基本上, 算法用于决策的判断条件是一个命题逻辑, 根据其真假可以判别. 这时候我们在前面的一些内容就派上用场了.
上面我们已经对每一个部分所有的语义简单进行了了解, 下面, 我们把它们组合, 嵌套起来, 看一看他们能够解决什么样的问题.
从一个很常见的问题开始: 冒泡排序.
2.10.4. 用上面的语句(可以画流程图)及其列举与嵌套, 完成排序问题:
(1)输入:长度为n的自然数序列S(假设其中没有重复元素).
(2)输出: 序列S’, 其元素与S完全一样, 但已从小到大排好序.
一个可能的设计方法如图2.5所示. 我们可以模拟执行它.
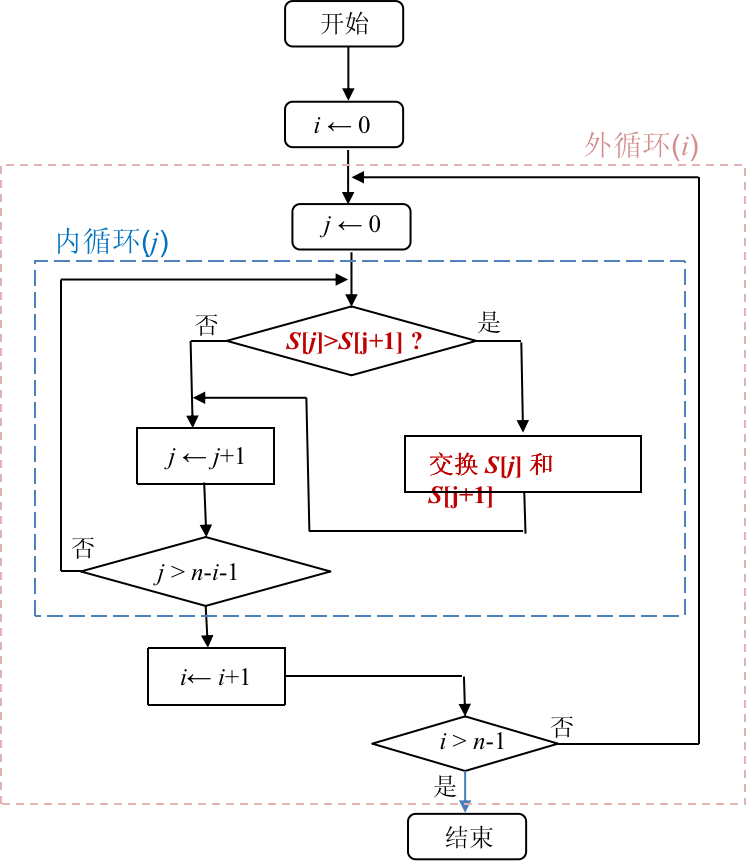
我们可以把内循环同样抽象成一个问题, 将一个子序列中的最大元素放到该子序列位置地址最大的地方(可以认为最后方). 那么对于它, 我们应该如何定义循环不变量?
每次i循环开始前序列 S 中地址最高的 i 个位置(除 i = 0 外, 即S[n −i] 到 S[n −1]) 包含 S 中前 i 个最大的元素, 且已从小到大排好序; 序列中其它位置上的元素即 S 中其它 n −i 个元素.
下面按照如下的三个方法归纳:
事实上, 把所有的内容嵌套起来就是我们构造很复杂的情形的一个基本的方法. 因此, 我们就把很多简单的过程通过这样的方式进行了组合.
如果我们通过“子问题拆解”的方法来做这件事, 有什么样的好处?
𝔹onus
在第一章里面我么说TRM里面有一条跳转指令, 为什么现在我们没有详细介绍goto指令, 并且绝大多数语言(除了C,C++)都没有了goto呢?
ℙassage
Go To Statement Considered Harmful(Cropped)
E.W. Dijkstra
from Communications of the ACM, Vol. 11, No. 3, March 1968, pp. 147-148
My first remark is that, although the programmer’s activity ends when he has constructed a correct program, the process taking place under control of his program is the true subject matter of his activity, for it is this process that has to accomplish the desired effect; it is this process that in its dynamic behavior has to satisfy the desired specifications. Yet, once the program has been made, the “making” of the corresponding process is delegated to the machine.
My second remark is that our intellectual powers are rather geared to master static relations and that our powers to visualize processes evolving in time are relatively poorly developed. For that reason we should do (as wise programmers aware of our limitations) our utmost to shorten the conceptual gap between the static program and the dynamic process, to make the correspondence between the program (spread out in text space) and the process (spread out in time) as trivial as possible.
......
The unbridled use of the go to statement has an immediate consequence that it becomes terribly hard to find a meaningful set of coordinates in which to describe the process progress. Usually, people take into account as well the values of some well chosen variables, but this is out of the question because it is relative to the progress that the meaning of these values is to be understood! With the go to statement one can, of course, still describe the progress uniquely by a counter counting the number of actions performed since program start (viz. a kind of normalized clock). The difficulty is that such a coordinate, although unique, is utterly unhelpful. In such a coordinate system it becomes an extremely complicated affair to define all those points of progress where, say, n equals the number of persons in the room minus one!
The go to statement as it stands is just too primitive; it is too much an invitation to make a mess of one’s program. One can regard and appreciate the clauses considered as bridling its use. I do not claim that the clauses mentioned are exhaustive in the sense that they will satisfy all needs, but whatever clauses are suggested (e.g. abortion clauses) they should satisfy the requirement that a programmer independent coordinate system can be maintained to describe the process in a helpful and manageable way.
......
In Guiseppe Jacopini seems to have proved the (logical) superfluousness of the go to statement. The exercise to translate an arbitrary flow diagram more or less mechanically into a jump-less one, however, is not to be recommended. Then the resulting flow diagram cannot be expected to be more transparent than the original one.
在程序变的更加复杂的时候, 程序就会变得像面条一样难以复杂.
之后文件夹下面就有一些.s文件了. 这是把C语言展开为了最基本的指令序列的结果. 可见, 当问题规模变得复杂的时候, 我们必须让复用重复的部分更加容易.
𝔹onus
所以, 用子过程有什么好处?
一个很好的问题是对于子过程, 什么会变, 什么不变? 一个可能的答案是代码的表现形式会变, 但是及其在外部看到的与其等价的形式是不会变的.
另外一个好处是子过程允许“自己调用自己”. 当然, 不加结束的自己调用自己会带来很多的问题. 比如, 下面的程序里面:
1 def call_myself(): 2 print("I am calling myself that cannot stop!") 3 call_myself()
注意到Python会抛出RecursionError. 如果是用C或者C++来写同样的东西, 可能就不是很友好了. 因为它只会卡住, 然后就有一个奇怪的返回值, 令人摸不着头脑.
在第一章我们用小纸条和老师以及作业本说明了什么是递归. 在这一节我们有一个更加重要的问题: 递归与数学归纳法有什么区别? 比如Hanoi塔问题:
2.11.1 (Hanoi塔问题). Object of the game is to move all the disks over to Tower 3 (with your mouse). But you cannot place a larger disk onto a smaller disk.
You may play it here: https://www.mathsisfun.com/games/towerofhanoi.html
现在我们来说一说数学归纳法到递归的一个关系:
数学归纳法. “假如”这个结论对k −1是成立的, 我试图证明它对k也是成立的. 如果我做到了, 就可以认为(当然考虑到“奠基”)对任意不小于奠基值的自然数结论都成立.
递归. “假如”有“人”能帮我解决规模为k −1的问题“实例”我就试图用那个结果来解该问题规模为k的“实例”; 如果我做到了, 就可以认为(当然也得给个“base case”的解法)我解了这个问题.
但是这样思维上看上去很自然, 我们到底要如何执行呢? 事实上, 就是我们使用的那个“作业与纸条”的例子. 我们用call stack以及程序执行当前行的“箭头”来进行计算.
𝔼xample:
计算机是如何执行Hanoi塔的递归程序的.
下面我们来看更多的例子.
今天我们希望生成10!的排列. 比如从1234567890一直生成到0987654321为止.
那么, 利用递归的思想很容易看出当n = 4时的结果和当n = 3时的结果是什么关系?
每一步有两种情形: 第一种是在前面加一个, 第二种是在后面加一个. 如我们有x, 接下来考虑加a, 那么有ax或者ax. 然后变为更加基础的情形.
我们会在下学期来进行更多的计算的细节. 例如均摊的分析, 摊还分析等手法.
与算法一起, 我们可以和计算机完成很多有趣的事情, 因此, 我们还需要学习更多的技巧, 让我们在后续的课程中学习更多的内容!
Real power can’t be given, it must be taken. – Godfather
–Georg Cantor
Point set topology is a disease from which the human race will soon recover. Later generations will regard Mengenlehre (set theory) as a disease from which one has recovered. –Henri Poincare
We are not speaking here of arbitrariness in any sense. Mathematics is not like a game whose tasks are determined by arbitrarily stipulated rules. Rather, it is a conceptual system possessing internal necessity that can only be so and by no means otherwise. –David Hilbert
在中学的时候, 我们定义的集合是如下的一个数学对象: 集合就是任何一个有明确定义的对象的整体.
𝔻ialogue
A: 这个定义看上去好有道理...
B: 其实集合大多数情况是不做定义的...
A: 为什么?
B: 其实原因是说了就不灵了... 一会回看到Russell悖论.
这也引出了概括原则:
很多时候我们需要判别两个集合是不是相等, 那么我们有外延性原理:
这条公理意味着集合这个对象完全由它的元素决定.
有时候我们需要从一个集合里面抽出一部分, 也就是寻找一个集合的子集. 因此我们有如下的定义.
我们还可以证明两个集合相等, 当二者互为对方的子集时候.
然后, 让我们来对于高中学习过的操作重新定义一下.
除此之外, 像命题逻辑一样, 集合也有一些运算的规律. 我们可以将它与命题逻辑一起观察, 并且发现其中的规律.
对于这样的命题, 我们同样给出证明.
. 对任意x,
| x ∈A ∪(B ∩C) | |||
| ⟺ | (x ∈A) ∨(x ∈B ∧x ∈C) | ||
| ⟺ | (x ∈A ∨x ∈B) ∧(x ∈A ∨x ∈C) | ||
| ⟺ | (x ∈A ∪B) ∧(x ∈A ∪C) | ||
| ⟺ | x ∈(A ∪B) ∩(A ∪C) |
同样, 像命题公式一样, 集合的运算也遵循吸收率:
. 对任意x,
| x ∈A ∪(A ∩B) | |||
| ⟺ | x ∈A ∨(x ∈A ∧x ∈B) | ||
| ⟺ | x ∈A |
有了这个我们就可以使用这个证明一个比较重要的习题.
.
首先证明左边的部分: 对任意 x ∈B
| x ∈B | |||
| | x ∈A ∨x ∈B | ||
| | x ∈A ∪B |
然后看另一个等价符号, 对于任意的x ∈A:
| x ∈A | |||
| | x ∈A ∧x ∈B | ||
| | x ∈A ∩B |
3.1.7 (绝对补 (Absolute Complement); A,A′,Ac). 设全集为U.
其中, 全集 U (Universe) 是当前正在考虑的所有元素构成的集合. 一般均默认存在. 通常可以注意到: 不存在“包罗万象”的全集.
和命题逻辑一样, 相对补和绝对补之间就像是命题符号一样, 存在一些联系.
. 对任意 x,
| x ∈A ∖B | |||
| ⟺ | x ∈A ∧x | ||
| ⟺ | x ∈A ∧(x ∈U ∧x | ||
| ⟺ | x ∈A ∧x ∈B | ||
| ⟺ | x ∈A ∩B |
. 对任意 x,
| x ∈A ∪B | |||
| ⟺ | x ∈U ∧¬(x ∈A ∨x ∈B) | ||
| ⟺ | x ∈U ∧x | ||
| ⟺ | (x ∈U ∧x | ||
| ⟺ | x ∈A ∧x ∈B | ||
| ⟺ | x ∈A ∩B |
. 我们只来证明第二个. 第一个是同理的.
| C ∖(A ∪B) | |||
| ⟺ | C ∩A ∪B | ||
| ⟺ | C ∩(A ∩B) | ||
| ⟺ | (C ∩A) ∩(C ∩B) | ||
| ⟺ | (C ∖A) ∩(C ∖B) |
这些命题的意义在于再证明集合相关的命题的时候, 就不需要从中抽出一个元素单独讨论了; 相反, 我们可以用集合整体的性质.
.
| C ∖(A ∪B) | |||
| ⟺ | C ∩A ∪B | ||
| ⟺ | C ∩(A ∩B) | ||
| ⟺ | (C ∩A) ∩(C ∩B) | ||
| ⟺ | (C ∖A) ∩(C ∖B) |
这里面有一个类似一个异或操作的运算符: 对称差.
既然集合的对象是一组元素, 那么集合也是对象, 集合中的元素自然也可以被传进去看作运算. 由此, 我们需要定义关于集合的集合的运算.
举一些例子, 比如𝕄 = {1,2},{{1,2},3},{4,5}
, 那么⋃
𝕄 =
1,2,3,4,5,{1,2}
.
注意元素只被解开了一次而不是一次解包到我们认为的“基本元素”. 因为有时候“基本元素”也是用集合定义的. 我们后来会发现我们可以把整个数学基础建立到集合论的基础上.
和求和记号一样, 为了方便书写, 我们也有类似的记号:
和广义并一样, 我们还有广义交. 定义如下:
同样的, 如果𝕄 = {1,2},{{1,2},3},{4,5}
是全集, ⋂
𝕄 = ∅. 同样只是展开一次就行了. 注意一个有趣的情况: ⋂
∅= U.
“包含所有元素的集合”在后面会发现会导出一个矛盾, 有时候我们也会认为这样说的结果是未定义的.
那么类似的, 我们也希望广义集合里面有没有像普通集合的一些操作. 答案是肯定的. 下面我们来探讨一些有趣的内容.
. 我们只来证明第二个. 第一个是同理的. 对任意 x,
| x ∈X ∖⋃ α∈IAα | |||
| ⟺ | x ∈X ∧¬(∃α ∈I. x ∈Aα) | ||
| ⟺ | x ∈X ∧(∀α ∈I. x | ||
| ⟺ | ∀α ∈I. (x ∈X ∧x | ||
| ⟺ | x ∈⋂ α∈I(X ∖Aα) |
我们同样可以用这条规律来化简集合, 而不用真正在一个集合的集合里面取出来一个元素.
𝔼xample:
如果
请化简:
.
| A | = ℝ ∖⋂ n∈ℤ+(ℝ ∖Xn) | ||
| = ℝ ∖ | |||
| = ℝ ∖ | |||
| = ℤ |
在高中, 我们学习了排列组合. 如果对于集合中的元素进行“选择性缺席”, 这样就可以让我们构造出更加复杂而全面的集合了.
这个之所以强大, 是因为给定一个A, 就有如下的内容可以被生成.
因为对于|A|= n的句子, |𝒫(A)|= 2n, 因此有时候也写做2A或者{0,1}A.
接下来看一个(看似)没啥用的定理:
这个定理的作用是在∈和⊆之间转换, 同时脱去一层𝒫()记号.
𝔼xample:
请证明:
. 根据上面的定理, 我们有
分别证明之:
| ∅∈𝒫(𝒫(S)) | |||
| ⟺ ∅⊆𝒫(S) |
| {∅}∈𝒫(𝒫(S)) | |||
| ⟺ {∅}⊆𝒫(S) | |||
| ⟺ ∅∈𝒫(S) | |||
| ⟺ ∅⊆S |
其实幂集生成之间也有一些关系. 不妨看一看.
. 对于任意 x,
| ⟺ x ∈𝒫(A) ∩𝒫(B) | |||
| ⟺ x ∈𝒫(A) ∧x ∈𝒫(B) | |||
| ⟺ x ⊆A ∧x ⊆B | |||
| ⟺ x ⊆A ∩B | |||
| ⟺ x ∈𝒫(A ∩B) |
. 对于任意 x,
| ⟺ x ∈⋂ α∈I𝒫(Aα) | |||
| ⟺ ∀α ∈I. x ∈𝒫(Aα) | |||
| ⟺ ∀α ∈I. x ⊆Aα | |||
| ⟺ x ⊆⋂ α∈IAα | |||
| ⟺ x ∈𝒫(⋂ α∈IAα) |
前面我们提到“不存在含有任何东西的集合”. 这就是我们以前知道的通俗讲述的“理发师悖论”. 形式化的, 根据概括原则, 如果性质P是P(x) ≜“xx”,
集合R = {x∣x
x}, 那么R ∈R 吗?
“悖论出现于数学的边界上, 而且是靠近哲学的边界上” — Godel
之后, 数学家们提出了ZF(ZFC)公理化集合论, 避免了这样的内容. 通过粗暴的避免了这种情况, 我们得到了一个还可以使用, 但是丧失了一部分确定性的集合.
我们在初中和高中的学习中学习了很多的“关系”. 比如, 比较两个数的大小, 我们引入了“大于”, “小于”和“等于”的关系. 这样的内容我们可以进一步的抽象, 提炼出“关系”的一些共性.
比如, 我们可以在ℝ上定义“Near”关系.
𝔼xample:
如果|a −b|< 1(a,b ∈ℝ), 则称a,b具有Near关系.
回顾我们学过的表达“关系”的运算符, 相当一部分满足下面的性质:
自反性.
对称性.
传递性.
很多时候, 我们把自反性 + 对称性 = 相容关系. 相容关系的含义其实是表明这两个关系之间有交叉.
这样, 我们就可以把关系表示成一个集合. 不严格的说, 在上面的定义中, 我们可以有这样的集合: R = {(a,b)∣|a −b|< 1}.
下面来看几个更多的例子. 比如整除关系.
𝔼xample:
假设X = {1,2,3,4,5,6,10,12,15,20,30,60}, “关系”是X 上的整除关系.
按照上面的展开, 我们就有所有整除的全体(有序对(a,b)表示的关系是a|b):
可以看到在上述的关系中, 上面的自反性, 对称性, 传递性仍然满足. 这种结构十分的常见. 比如地图上面的地方的“可达”关系, 还有给定集合的幂集按“包含”关系排序, 自然数按照大小关系排序, 等等. 满足上述的三条性质的关系叫做“偏序关系”. 特殊的, 我们或许还会发现自然数可以唯一地按照大小被排成一排, 这是一种比较特殊的偏序关系, 后来我们会定义它为全序关系.
特别的, 我们可以把上述偏序关系画成一张图, 也就是在多个维度上都有不同的序, 因此没办法唯一的列成一列, 包含所有元素.
比如上述的幂集的例子, 化作一张图3.1所示:
观察正整数集, 发现这是一条链式结构, 它和上述的偏序集最大的区别是什么呢? 其实, 最大的区别是在整数中的大于关系存在“连接性”.
连接性.
也就是自反性 + 反对称性 + 传递性 + 连接性 = 全序关系.
我们可能会很自然的想(a,b) = (c,d) ⟺ a = c ∧b = d, 对于这样自然产生的概念, 我们同样要将它严格化, 给出一个定义.
历史上, 很多人会用集合的观念来刻画有序对. Norbert Wiener在1914年给出了这样的定义.
这样一来, 有序对之间的相等关系看上去就自然了很多.
. 也就是证明
我们有:
| ⟺ | ({a}= {c}∨{a}= {c,d}) ∧({a,b}= {c}∨{a,b}= {c,d}) | ||
| ⟺ | ({a}= {c}∧{a,b}= {c}) ∨ | ||
| ({a}= {c}∧{a,b}= {c,d}) ∨ | |||
| ({a}= {c,d}∧{a,b}= {c}) ∨ | |||
| ({a}= {c,d}∧{a,b}= {c,d}) |
有了有序对, 我们还可以把它拓广到n个元素的情况. 于是我们有定义:
在这个结构上同样是可以应用数学归纳法的. 不过一般我处理而二元组就行了. 多数情况下, 我们仅处理“二元关系”, 因此也仅使用“有序对”
如果我们有两个集合, 从两个集合中各取得一个元素, 把它们组合成一个有序对,塞到一个新的集合里面, 这样, 我们就可以对于集合做一点组合, 生成更加复杂的集合了. 这样的操作叫做笛卡尔积.
那么“笛卡尔积”这个操作满足哪些运算律呢? 我们首先来考察一些例子.
𝔼xample:
| X ×∅= ∅×X | ||
| X ×Y ≠Y ×X | ||
| (X ×Y ) ×Z ≠ X ×(Y ×Z) | ||
| A = {1} (A ×A) ×A ≠ A ×(A ×A) |
我们发现这个符号既没有普遍的交换律, 也没有普遍的结合律. 但是是有分配律的.
下面我们来以证明A ×(B ∩C) = (A ×B) ∩(A ×C)为例, 看一下这个是如何进行起作用的.
. 对任意有序对 (a,b),
| (a,b) ∈A ×(B ∩C) | |||
| ⟺ | a ∈A ∧b ∈(B ∩C) | ||
| ⟺ | a ∈A ∧b ∈B ∧b ∈C | ||
| ⟺ | (a ∈A ∧b ∈B) ∧(a ∈A ∧b ∈C) | ||
| ⟺ | (a,b) ∈A ×B ∧(a,b) ∈A ×C | ||
| ⟺ | (a,b) ∈(A ×B) ∩(A ×C) |
同样的, 我们可以有多个元素的笛卡尔积.
回想我们从数轴到平面直角坐标系再到空间直角坐标系, 我们可以发现这样的过程也就是对于一个维度反复做笛卡尔积的结果.
但在本节的情况下, 我们仅处理“二元关系”, 因此也仅使用“二元笛卡尔积”.
我们以前做了有关关系的定义, 但是我们可能还要给“什么是关系”在集合方面下一个稍微集合化的定义. 于是我们有定义:
3.4.5 (关系 (Relations)). A relation R from A to B is a subset of A ×B:
Sepcially, if A = B, R is called a relation on A.
为了简化符号, 我们有时候也通过这样的方式来书写:
举一些例子: A ×B 和 ∅都是从 A 到 B 的关系, 前者的意义是任意两个A和B中的元素都有关系, 后者是都没有关系. 回顾我们在小学中学更一般的关系, 我们就会发现有更加有趣的二元关系:
在生活中更有这样的关系. 比如P是所有人的集合, 如果我们定义M = {(a,b) ∈P ×P∣a is the mother of b}, B = {(a,b) ∈P ×P∣a is the brother of b}, 那么上述定义的M和B都满足“关系”的定义.
有了这样的抽象, 我们就可以很开心的研究另外一些更重要的问题了. 具体地, 我们要研究这些重要的关系:
在进行之前, 我们认为对于关系的运算进行一些内容.
总体而言, 在这一小节中我们会给出三个定义, 5个操作, 以及7个对应的性质.
其实, 这一节的内容很大程度上和中学定义的函数类似. 但是有一个重大的区别. 从现在开始, 我们稍微忘记我们高中关于“函数”的定义, 但是留下“函数”带给我们的思考方式. 下面我们来用有序对重新解释这一切.
我们在函数中说“定义域”是函数中有定义的地方的横坐标构成的集合, 在这里面的∃b就保证了在这个点一定被定义了, 那么我们就取出来它的a(横坐标). “扫描”所有这样的有序对(a,b)并将满足条件的a取出来, 我们就完成了这样类似概念的迁移.
我们在函数中说“值域”是函数中所有有定义的横坐标所对应的纵坐标, 在这里面的∃a就说明了有这样的点被取到, 那么我们就取出来它的b(横坐标). “扫描”所有这样的有序对(a,b)并将满足条件的b取出来, 同样有类似的概念.
定义域和值域并起来就是域. 这样可以让我们直观的明确了解“二元关系”之间的空间映射关系.
举个例子: 对于R = {(x,y)∣x2 + y2 = 1}⊆ℝ ×ℝ, 它的dom(R) = [1,1], ran(R) = [−1,1], fld(R) = [−1,1].
我们来看一个更抽象的. 不过别忘了本质上就是用集合的操作解决这一切问题.
. 对任意 a,
| a ∈ dom(R) | |||
| | ∃b. (a,b) ∈R | ||
| | ∃b. {{a},{a,b}}∈R | ||
| | ∃b. {a,b}∈⋃ R | ||
| | ∃b. a ∈⋃ ⋃ R | ||
| | a ∈⋃ ⋃ R |
这个例子的直观解释就是任何的定义域, 值域都会在二元组的某一个元素中“出现”.
1. 逆变换. 像“反函数”的概念一样, 关系有时候也有逆变换.
我们可以来看几组例子:
直观地, 我们自然会想到反关系的反仍然是原来的关系. 所以我们有如下定理:
. 对任意 (a,b),
| (a,b) ∈(R−1)−1 | |||
| ⟺ | (b,a) ∈R−1 | ||
| ⟺ | (a,b) ∈R |
既然关系也是集合定义的, 那我们自然可以证明它的交, 并, 补. 在我们做的有益的探索中, 我们会发现这个定理还是比较重要的.
2. 限制. 由于问题的定义和性质, 有时候我们可能需要对于构造的“全面”集合的状态空间进行“裁切”, 来打造更精细的集合. 这样就可以自然地引入集合的限制操作. 我们希望引入这样的记号, 使得它可以对于这个关系二元组(a,b)中的a, b分别加以筛选. 于是我们有定义:
3.4.11 (左限制 (Left-Restriction)). Suppose R ⊆X ×Y and S ⊆X. The left-restriction relation of R to S over X and Y is
3.4.12 (右限制 (Right-Restriction)). Suppose R ⊆ X ×Y and S ⊆ Y . The right-restriction relation of R to S over X and Y is
哎呀! “限制”和“左限制”的记号重复了! 但是仔细看一下他们的前提是不一样的. “左限制”的前提是有R ⊆X ×X, 而“限制”的前提是R ⊆X ×X, 也就是自己集合中元素到自己集合元素的关系.
下面我们来看刚刚举的例子: 如果R = {(x,y)∣x2 + y2 = 1}⊆ℝ ×ℝ, R| ℝ+的含义就是表示关系的二元组(a,b)中, a只取ℝ+的时候满足的才被认为“满足”关系.
𝔹onus
对于这样的情况, 我们能不能使用xOy平面表达这种关系呢? 限制在平面上的意义是什么?
3. 像(Image). 想一想这种“有所对应”的感觉, 好像在高中学习函数那一节里面见过类似的, 也就是有点像函数里面f()做的事情. 同样的, 这里面也有类似描述这样一种“有所对应”的定义.
为了简化符号, 一般而言R[a] ≜R[{a}] = {b∣(a,b) ∈R}.
4.逆像. 同样的, 我们有时候可能需要顺藤摸瓜, 这就自然地导出了像也有“逆”的概念.
同样为了简化记号, 我们有R−1[b] ≜R−1[{b}] = {a∣(a,b) ∈R}.
有了这两个操作之后, 事情就变得复杂了. 比如R−1[R[X]]和X的关系如何, R[R−1[Y ]]和Y 的关系又如何? 经过证明, 我们给出如下的定理:
5. 复合. 像复合函数一样, 这是一种构建复杂系统的很好的一种方法. 因此我们自然给出定义:
3.4.16 (复合 (Composition; R ∘S, R;S)). The composition of relations R ⊆ X ×Y and S ⊆ Y ×Z is the relation
举个例子, R = {(1,2),(3,1)} S = {(1,3),(2,2),(2,3)}, 那么R ∘S = {(1,1),(2,1)}, S ∘R = {(1,2),(1,3),(3,3)}. 因为这个和“乘法”比较相似, 有时候我们也用空心圆圈表示. R(2) ≜R ∘R = {(3,2)}, (R ∘R) ∘R = ∅.
𝔹onus
有的人习惯记号A ∘B ∘C = A ∘(B ∘C), 还有的人习惯A ∘B ∘C = (A ∘B) ∘C. 这样做有区别吗?
. 对任意 (a,b),
| (a,b) ∈(R ∘S) ∘T | |||
| ⟺ | ∃c. | ||
| ⟺ | ∃c. | ||
| ⟺ | ∃d. ∃c. | ||
| ⟺ | ∃d. | ||
| ⟺ | ∃d. | ||
| ⟺ | (a,b) ∈R ∘(S ∘T) |
这就表明关系的复合满足结合律, 但是不满足交换律(和矩阵乘法很相似).
. 对任意 (a,b),
| (a,b) ∈(R ∘S)−1 | |||
| ⟺ | (b,a) ∈R ∘S | ||
| ⟺ | ∃c. (b,c) ∈S ∧(c,a) ∈R | ||
| ⟺ | ∃c. (c,b) ∈S−1 ∧(a,c) ∈R−1 | ||
| ⟺ | (a,b) ∈S−1 ∘R−1 |
1. 自反的.
举几个例子:
其实所有自反的关系都是这个关系的一个子集, 可以有如下的表达.
2. 反自反.
同样的, 我们给一些例子:
3. 对称.
对称就意味着R的逆是的形式是很好的. 具体的, 有如下定义.
4. 反对称.
例如>, |都具有反对称性.
5. 传递性
有了传递性, 有时候就意味着关系的封闭性.
. 对任意 (a,b),
| (a,b) ∈R ∘R | |||
| | ∃c. (a,c) ∈R ∧(b,c) ∈R | ||
| | (a,b) ∈R |
对任意 a,b,c
传递性和上面的内容一起构成了“序关系”. 上回我们定义了“偏序关系”. 接下来看到“偏序关系”到全序关系的重要关系, 就是下面的一个内容.
6. 连接性.
我们发现, 在以前我们涉及“关系”的比较重, a > b, b < a, b = a三种关系中, 有且只有一种关系成立. 这样我们可以抽象出“三分的”性质.
7. 三分的.
其实这些关系是可以刻画“求逆”的可行性和唯一性. 具体的, 有如下的定理.
. 对任意 (a,b),
| (a,b) ∈R ∘R | |||
| | ∃c. (a,c) ∈R ∧(b,c) ∈R | ||
| | (a,b) ∈R |
我们很多时候都在说“等价”, 一个很重要的问题是什么是等价? 我们可以运用什么样的语言去刻画它? 这一节, 我们来简单描述这样的特殊的二元关系 – 等价关系.
很多时候, 我们在研究数学关系会发现很多相同点. 比如在模意义下, 很多数是相等的. 比如3 ≡6 mod 3. 他们的余数都是0. 这就有一个很有趣的相似关系了.
用同余的例子, 我们会发现这种“等价性”满足这样几条性质:
3.5.1 (Equivalence Relation). R ⊆X ×X is an equivalence relation on X iff R is
更一般的, 我们发现各个等价关系其实把整个区间“划分”成了不同的区域, 其中每一个区域里面都有和其他地方在某些意义下完全相同的特性.
就像我们把所有属于中国的领土通过“划分”的方式形成了省, 其中每个省都有自己的地方行政机关, 他们彼此等价. 因此, 我们可以说这个是在中国领土上划分的情况下, 行政机关的等价关系.
更具体的, 划分有如下定义:
3.5.2 (划分 (Partition)). A family of sets Π = {Aα∣α ∈I} is a partition of X if
那么, 将划分的结果, 把每一类处于“等同地位的元素”拿出来看, 就可以被称作等价类了. 等价类其实可以看作拉拢所有的等价关系. 正式的, 我们有如下的定义:
为什么等价类如此重要? 一个原因是它提供了一个抽象, 让我们方便的研究很多问题.
像整数的模运算一样, 我们在“集合”的也想有类似的运算. 因此我们有“商集”的概念. 这样我们就可以把所有相互等价的元素取用出来, 进行研究.
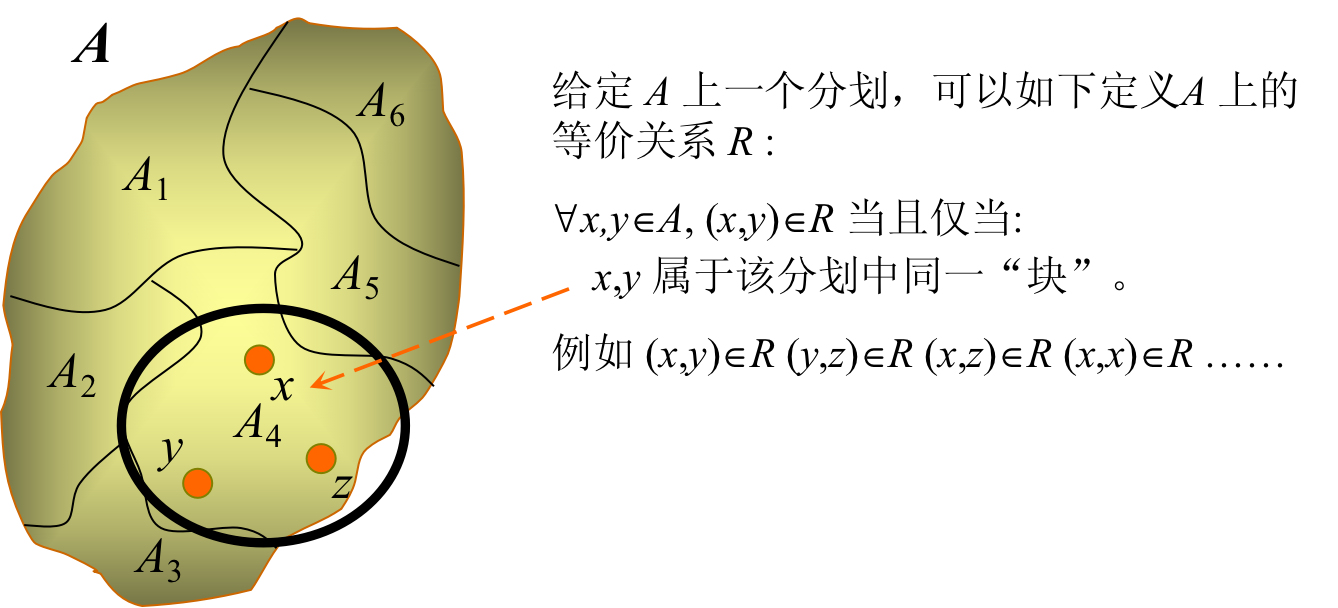
同样的, 这样取, 只不过是用另外一种维度划分(如图3.2)整个集合罢了. 这在直觉上看起来是对的, 下面我们来做一下证明.
. ∀a ∈X. [a]R≠∅,
∀a ∈X. ∃b ∈X. a ∈[b]R. □
在等价关系中, 下面这个定理可以很方便的从三个不同的侧面刻画“划分”, 同时帮助我们更容易的证明某些由“划分”产生的等价性问题.
. ∀a ∈X,b ∈X. [a]R ∩[b]R≠∅→[a]R = [b]R
一方面, 不妨设 x ∈[a]R ∧[b]R
| x ∈[a]R ∧[b]R | |||
| | aRx ∧xRb | ||
| | aRb |
另一方面, 对于任意 x,
| x ∈[a]R | |||
| ⟺ | xRa | ||
| ⟺ | xRb | ||
| ⟺ | x ∈[b]R |
这就意味着我们的划分在某种意义上也是一个等价关系!
3.5.5. If partition Π of X Equivalence Relation R ⊆X ×X, (a,b) ∈R ⟺ ∃S ∈Π. a ∈
S ∧b ∈S, R = {(a,b) ∈X ×X∣∃S ∈Π. a ∈S ∧b ∈S}
首先, 我们尝试把自然数的定义奠定在集合论的基础上. 具体的, 定义有如下的两条:
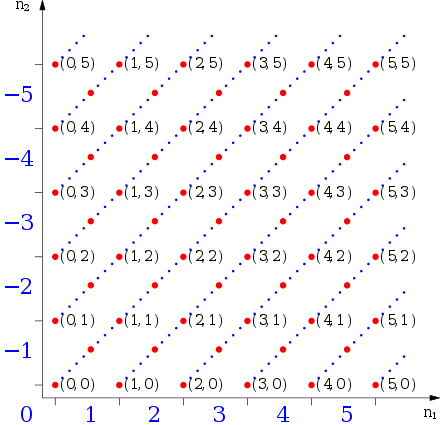
下面我们来定义一个关系∼, 在ℕ ×ℕ的集合上.
那么, ℕ×ℕ∕ ∼是什么呢? 哪些在∼环境下是什么样的情况呢? 发现, 只有负数加正数才可以化为等价类. 那么我们就可以说[(1,3)]∼这一类集合(1,3),(2,4),就定义为了负数−2.
于是相仿的, 我们就可以定义出ℤ. 形象的可以理解为图3.3.
有了整数, 我们就要为整数定义对应的加法和乘法. 分别记作+ℤ和×ℤ. 这样就可以让这个加法和乘法不会因为牵涉了自然数变得“有问题”.
现在我们假设我们的整数已经很好的定义了. 直接沿用其记号, 并且忘记刚刚的所有记号. 接下来我们再定义一个关系∼(和刚刚的内容不一样). 这个关系是定义在ℤ ×(ℤ ∖{0ℤ})上的.
那么请问ℤ ×(ℤ ∖{0ℤ})∕ ∼是什么?
如何用有理数定义实数? 请参见《数学分析》Dedekind分割.
如果我们把上一节中的“传递性”去掉, 我们就得到了相容关系. 通俗的讲, 相容关系指的是“如果A和B有这个关系, 那么B和A也有这样的关系”. 也就是二者是“相互作用的”. 例如, 朋友关系. A和B是朋友, 那么B和A也是朋友; 如果A和C是朋友, 我们不一定能够推出B和C也是朋友. 于是我们给出相容关系的定义.
3.6.1 (Compatibility relation). R ⊆X ×X is an compatibility relation on X iff R is
由于我们通常是对于一个集合来做这样的“相容关系”的定义的, 于是, 我们就希望用一个具体的例子说明这个关系到底在做什么.
我们可以发现集合的覆盖是不唯一的, 并且我们发现任意一个覆盖, 如果我们把每一个覆盖的Ai与他自己做笛卡尔积, 并且最终把它并起来, 事实上就得到了原来的集合的一个相容关系.
3.6.1. 给定一个集合A的一个覆盖S = {A1,A2,,An}, 有R = {A1,A2,
,An}, 则R = A1 ×A1 ∪A2 ×
A2 ∪
∪An ×An, 那么我们说R是A上的相容关系.
函数不允许一对多, 这就是它和“关系”最大的去区别.
回想我们以前学习过的东西, 好像“关系”和方程的图像有点相似. 也就是我们在高中的时候在平面直角坐标系中做的椭圆的图线: x2∕a2 + y2∕b2 = 1(a,b > 0). 接下来, 我们不妨来看一种特殊的“关系”: 函数.
𝔹onus
为什么函数不允许“一对多”? 在定义上有什么合理性?
让我们重新定义一下以前学过的函数.
在函数中, 除了定义域和值域之外, 还有陪域. 通常被称作“cod”. 比如对于一个映射(函数)f : A →B, dom(f) = A,cod(f) = B, 对于一个函数的值域ran(f) = f(A) ⊆B.
为什么这样定义? 值域为什么不是B? 原因是很多时候函数的值域难以求解, 这样就使得我们的表达造成很多不便. 而且很多时候如果强行把B当作值域很多时候可能会出现运算不封闭的问题, 在研究某些问题的时候非常不方便. 因此, 我们不妨把这个值域扩大一些, 这样才可以更方便一些. 因此, B就叫做“陪域”. 值域只不过是陪域的一个子集.
对于证明而言, 我们同样有一套形式化的证明语言: ∀a ∈A.,∀a ∈A. ∃b ∈B.(a,b) ∈f,∃!b ∈B.,∀b,b′∈B. (a,b) ∈f ∧(a,b′) ∈f b = b′.
当然我们可以看一些有趣的函数.
1. 恒等函数. “恒等”在数学的各个领域里面都是重要的. “恒等函数”的地位有时候和加法意义下的‘0’, 乘法意义下的‘1’很相似, 其特点是经过一次复合之后还是一样的. 我们一般用IX表示, I的意思是identity的缩写. 其中,
𝔽un fact
Weierstrass构造了一个处处连续, 处处不可导的函数.
其中, 0 < a < 1, b is a positive odd integer, ab > 1 + π.
当然, 我们也可以把相似的函数放在一个集合里面.
举一些例子, |X|= x,|Y |= y,|Y X|= xy.
𝔼xample:
类似的, 我们可以问: 是否存在由所有函数组成的集合? 像Russell一样, 我们的答案是否定的.
. Suppose by contradiction that A is the set of all functions. For every set X, there exists a function I{X}: {X}→{X}.
既然函数和集合的结论如此相似, 我们自然地想到函数有没有和集合一样的性质?
注意定义并没有要求陪域相同, 只要f = g ⟺ ∀(a,b). ((a,b) ∈f ↔(a,b) ∈g)满足, 我们就认为这是相等的.
既然是集合, 我们就要考察一些集合的运算. 如果f和g是函数, f ∩g,f ∪g是函数吗? 因此我们有如下的定理:
举几个例子. 如果我们有f : 𝒫(ℝ) →ℤ, f(A) = . 注意ℕ的良序原理, dom(f)∩dom(g) = ∅.
Dichlet函数也可以看作函数的并. 它是f : ℝ →ℝ的一个映射. 表达式写做: D(x) =
注意到这个函数是“处处不连续”的.
有时候函数之间的映射关系也是重要的. 比如, f : A →B, A在B中的对应元素是不是都是不同的? B中的元素有没有全部对应上A中的元素(可能不止被对应了一次)? A有没有和B中元素一一对应? 这样我们就有了单射, 满射的概念.
对于证明而言, 我们可以这样写: ∀a1,a2 ∈A. f(a1) = f(a2) →a1 = a2. 证明一个函数不是单射函数, 就可以这样写: ∃a1,a2 ∈A. a1≠a2 ∧f(a1) = f(a2).
同样的, 对于证明给定的函数是满射而言, 我们可以这样写: ∀b ∈B. ∃a ∈A. f(a) = b
, 反之, 我们可以这样写:
∃b ∈B.
∀a ∈A. f(a)≠b
.
既是双射又是满射的函数一定很特殊, 因为它有一个一一对应的关系. 因此我们给出如下定义:
那么, 一个集合和它的幂集之间可不可以找到一个满射呢? 其实是不行的. Cantor给出了一个证明.
. Let A be the set and let f : A → 2A. To show that f is not onto, we must find B ∈2A(i.e.B ⊆A) for which there is no a ∈A with no f(a) = B. In other words, B is a set that f “misses”. To this end, let
We claim there is no a ∈A with f(a) = B. Suppose, for the sake of contradiction, there is an a ∈A such that f(a) = B, we pounder: Is a ∈B?
To sum up, it can’t be onto. □
除了反证之外, 还有一个构造性的证明, 我们一并给出.
对角线论证 (Cantor’s diagonal argument). 以下仅适用于可数集合 A.
| a | ||||||
| 1 | 2 | 3 | 4 | 5 | ||
| 1 | 1 | 1 | 0 | 0 | 1 | |
| 2 | 0 | 0 | 0 | 0 | 0 | |
| 3 | 1 | 0 | 0 | 1 | 0 | |
| 4 | 1 | 1 | 1 | 0 | 1 | |
| 5 | 0 | 1 | 0 | 1 | 0 | |
| | ||||||
和关系一样, 函数也有限制等操作. 我们来看看.
注意X ⊆A并不是必要的(虽然平时经常这样用).
同样, X ⊆ dom(f) = A也不是必要条件, 尽管通常是这样的. 记号层面, f({a}) = {b} 简记为 f(a) = b.
也就是y ∈f(X) ⟺ ∃x ∈X. y = f(x).
注意不一定要Y ⊆ ran(f), 但是很多情况都是满足这样的. 但是注意
想一想, 为什么会这样?
这样一来, 我们就有这样的关系 :y ∈f(X) ⟺ ∃x ∈X. y = f(x),x ∈f−1(Y ) ⟺ f(x) ∈Y .
需要注意的是, 如果有f : a →b, a ∈A0 f(a) ∈f(A0), 这个式子才可以成立: a ∈A0 ∩ A
f(a) ∈f(A0).
关于求逆也有很多的性质. 很多时候我们可能会想当然的误用. 所以使用之前一定要小心, 小心, 再小心.
幸运的是, 它还保留有很多性质. 我们一一罗列, 并给出一些证明.
3.7.6 (Properties of f and f−1).
f preserves only ⊆ and ∪:
f−1 preserves ⊆, ∪, ∩, and ∖:
对于A1 ⊆A2 f(A1) ⊆f(A2), 证明如下:
.
| b ∈f(A1) | |||
| ⟺ | ∃a ∈A1. b = f(a) | ||
| | ∃a ∈A2. b = f(a) | ||
| ⟺ | b ∈f(A2) |
对于f(A1 ∩A2) ⊆f(A1) ∩f(A2), 证明如下. 注意是哪一步变换, 使得它的箭头方向变为单向了, 为什么?
. 对任意 b,
| b ∈f(A1 ∩A2) | |||
| ⟺ | ∃a ∈A1 ∩A2. b = f(a) | ||
| | |||
| ⟺ | b ∈f(A1) ∧b = f(A2) | ||
| ⟺ | b ∈f(A1) ∩f(A2) |
对于f(A1 ∖A2) ⊇f(A1) ∖f(A2) :
. 对任意 b,
| b ∈f(A1) ∖f(A2) | |||
| ⟺ | b ∈f(A1) ∧b | ||
| ⟺ | (∃a1 ∈A1. b = f(a1)) ∧(∀a2 ∈A2. b≠f(a2)) | ||
| | ∃a ∈A1 ∖A2. b = f(a) | ||
| ⟺ | b ∈f(A1 ∖A2) |
对于B1 ⊆B2 f−1(B
1) ⊆f−1(B
2), 证明如下:
. 对任意 a,
| a ∈f−1(B 1) | |||
| ⟺ | f(a) ∈B1 | ||
| | f(a) ∈B2 | ||
| ⟺ | a ∈f−1(B 2) |
对于f−1(B 1 ∩B2) = f−1(B 1) ∩f−1(B 2), 证明如下:
. 对任意 a,
| a ∈f−1(B 1 ∩B2) | |||
| ⟺ | f(a) ∈B1 ∩B2 | ||
| ⟺ | f(a) ∈B1 ∧f(a) ∈B2 | ||
| ⟺ | a ∈f−1(B 1) ∧a ∈f−1(B 2) | ||
| ⟺ | a ∈f−1(B 1) ∩f−1(B 2) |
对于A0 ⊆A A0 ⊆f−1(f(A
0)), 有
. 对任意 b,
| a ∈A0 | |||
| | a ∈A0 ∩ A | ||
| | f(a) ∈f(A0) | ||
| ⟺ | a ∈f−1(f(A 0)) |
对于B0 ⊇f(f−1(B 0)), 思考什么时候这个条件是充要的( ⟺ )?
. 对任意 b,
| b ∈f(f−1(B 0)) | |||
| ⟺ | ∃a ∈f−1(B 0). b = f(a) | ||
| ⟺ | ∃a ∈A. f(a) ∈B0 ∧b = f(a) | ||
| | b ∈B0 |
“iff” when f is surjective and
. □
作为化简单为复杂的利器, 和关系一样, 函数也有复合.
𝔹onus
回顾关系复合的定义: The composition of relations R and S is the relation
和函数的有什么不同? 为什么是存在?
. 我们只需证明:
对于(h ∘(g ∘f))(x) = ((h ∘g) ∘f)(x):
| (h ∘(g ∘f))(x) | |||
| = | h((g ∘f)(x)) | ||
| = | h(g(f(x))) |
| ((h ∘g) ∘f)(x) | |||
| = | ((h ∘g)(f(x))) | ||
| = | h(g(f(x))) |
对于第一条, 我们写出“injective”的定义, 然后完成逻辑推演.
.
| (g ∘f)(a1) = (g ∘f)(a2) | |||
| ⟺ | g(f(a1)) = g(f(a2)) | ||
| | f(a1) = f(a2) | ||
| | a1 = a2 |
对于第二条, 我们写出“surjective”的定义.
.
对于第三条, 如出一辙.
. 对任意 a1,a2,
| f(a1) = f(a2) | |||
| | g(f(a1)) = g(f(a2)) | ||
| | (g ∘f)(a1) = (g ∘f)(a2) | ||
| | a1 = a2 |
因为(1)和(2)很像, 因此只证明(2). 注意充要条件是在哪一步消失的.
. 对任意 a1,a2,
| g ∘f is surjective | |||
| ⟺ | ∀c ∈C. ∃a ∈A. (g ∘f)(a) = c | ||
| ⟺ | ∀c ∈C. ∃a ∈A. g(f(a)) = c | ||
| | ∀c ∈C. ∃b ∈B. g(b) = c | ||
| ⟺ | g is surjective |
什么时候有反函数? 反函数具有哪些性质? 在高中的时候老师可能不会和我们讲, 现在我们来探索一下反函数的性质.
3.7.11 (反函数 (Inverse Function)). Let f : A →B be a function.
The inverse of f is a function from B to A, denoted f−1 : B →A
if f is bijective.
We call f−1 the inverse function of f.
下面这个定理展示了什么时候具有反函数.
. By contradiction. Omitted. □
这些定理是帮助我们找到反函数/说明反函数不存在的一些好的结论.
对于(1).
. 对任意 b ∈B,
Suppose that a = f−1(b)
对于(2).
. g = (f−1 ∘f) ∘g = f−1 ∘(f ∘g) = f−1 ∘I B = f−1 □
我们当然可以看一看反函数的复合是怎样的一个情况. 1
那么, 我们就从集合论的角度构建了我们高中学习过的内容.
𝔻ialogue
你非常熟悉的实数集上的“不大于”关系和非空集合A的幂集合上定义的“子集”关系都是次序关系这与你长期以来的“commonsense”有差异吗
前面我们提到过偏序关系. 我们给出一个定义:
(1)自反的(∀x ∈X,x ≼x),
(2)对称的(∀x,y ∈X,x ≼y ∧y ≼x →x = y)
(3)传递的(∀x,y,z ∈X.x ≼y ∧y ≼z →x ≼z), 就称作R是A上的偏序关系. 通常记为≼. 整个序关系可以写作(X,≼)
𝔹onus
有没有一种直观的方法来表达这种情形? 或许我们可以把每个元素化作圆圈, 有这样的关系就把他们之间画一个箭头.
我们发现任意的一个关系, 我们都可以这样表示. 特别的, 对于一个偏序关系而言, 我们发现:
我们发现, 这样子表示还是有点麻烦了. 我们有没有办法来简化这一个事实呢? 我们其实可以按照下面的方法简化一下这个图:
这样的情形, 我们可以把偏序关系使用有向无环图(directed acyclic graph) 表示. 这样的一种可达(reachability)关系表示.
𝔹onus
与一般的关系图相比Hasse图简化了什么为什么可以简化
在我们日常的使用大于等于, 小于等于这样的元素的时候, 我们通常会注意到基本上这些内容都是可以取等的, 这就意味着满足这样的条件的集合中是有最大元和最小元的. 更一般地, 我们需要思考这些问题:
直观上, 我们会认为定义一个偏序集的上述内容是像图3.5这样的. 在上面的那一圈(没有连出的)定义为极大元, 最下面的一圈(没有连入的一圈)定义为极小元.
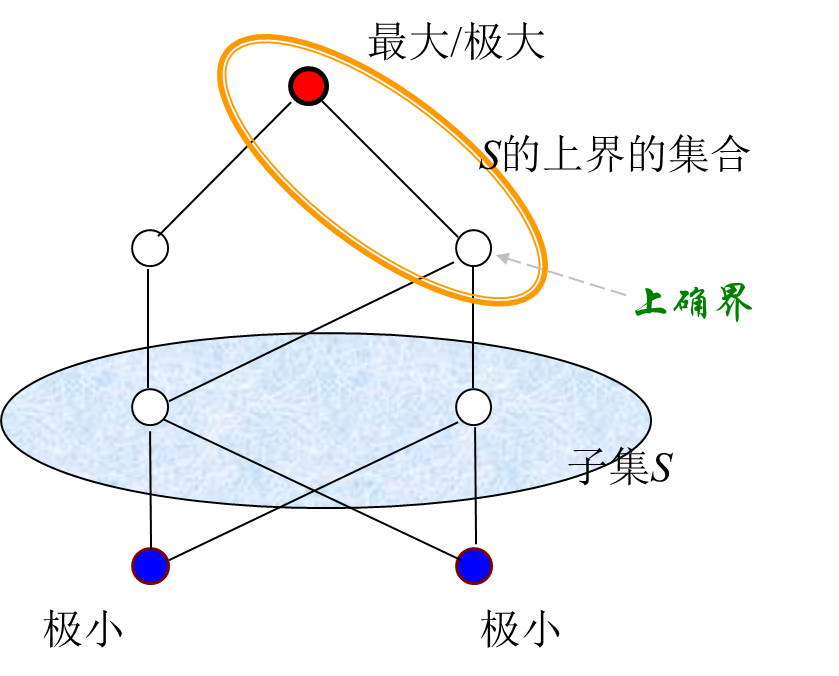
于是我们给出如下的定义:
3.8.2 (偏序集的极大元, 极小元). 令≼⊆X ×X是X上的偏序. 设a ∈X:
𝔹onus
极大元/极小元是不是总是存在的? 如果存在, 是不是唯一的?
我们来举几个例子. 比如(R,≤)的关系中, 没有极大元, 也没有极小元. 在除去0, 1整数的整除关系中, 有无穷多个极小元(质数), 没有极大元. 所以, 极大元, 极小元不总是存在的, 即使存在, 也不一定是唯一的. 但是在有限集的时候还是一定存在的. 我们后面会给出若干的证明.
. 假设(S,≼)是偏序集, 取任意的a1 ∈ S, 若对于任意的t ∈ S, a1 ≼ t, a1是极小元, 否则, 必有a2≠a1,且a2 ≼ a1, 若对任意t ∈
S ∖{a1}, a2 ≼ t, 则a2是极小元, 过程终止. 一般而言若遇到的a1,a2,,ai都不是极小元, 一定有ai+1是{a1,a2,
,an−1}.
但S是有限集, 这个过程一定会在某个ak(k = 1,2,
,n)上终止, 此时ak是极小元. □
𝔹onus
最大元/最小元是不是总是存在的? 如果存在, 是不是唯一的?
我们发现最大元和最小元不总是存在的–上面的一些例子已经足以说明了. 从字面的意思上, 我们可能会猜测最大元和最小元一但存在, 一定唯一. 下面我们来说明这件事情是对的.
. 假设存在两个不同的最大元x,y. 那么根据定义, 取得特殊的两个元素: x ≼y∧y ≼x, 根据偏序关系的反对称性, 立即得到x = y. 因此与假设矛盾. □
3.8.5 (最小上界(least upper bound)). 设(X,≼)是偏序集, 对于Y ⊆X, x ∈x是Y 的上界, 对于Y 的所有上界x′, 若有x ≼ x′, 则称x是Y 的最小上界.
3.8.6 (最大下界(greatest upper bound)). 设(X,≼)是偏序集, 对于Y ⊆ X, x ∈ x是Y 的下界, 对于Y 的所有下界x′, 若有x′≼x, 则称x是Y 的最大下界.
有些时候, 我们对于“有界”的东西十分的喜欢. 我们把任意两个元素之间都有最小上界和最大下界的这样的结构叫做“格(lattice)”.
我们刚刚说到的集合的(真)包含关系, 以及大于1的整数上的整除的关系来看, 上面讨论的两个例子都是格. 特殊的, 自然数上小于关系构成的内容也是格.
我们接下来对于一些概念加以定义. 比如, 有了≤, 自然会问一问会不会定义<.
有时候, 我们希望对于偏序集的内容比较大小, 因此, 对于一个偏序集而言, 我们有
我们发现所有链的集合或者所有反链的集合与集合包含关系也构成一个偏序集因此同样也可以讨论极大/极小、最大/最小链或反链.
大约在上个世纪, Dilworth就发现了S可以划分为k个元素互不相交的链的条件: 那就是
这是一个对偶关系(阐述的链与反链的关系), 我们可以使用归纳法来证明.
我们来举个例子: 与整除关系相关的链与反链.
𝔼xample:
定义N ∖{0}上的整除关系R : aRb 当且仅当存在t ∈N ∖{0}满足at = b (通常记为a|b). 那么关系R是偏序关系. 对偏序集 (N ∖{0},|) 考虑如下的问题
我们发现, 在无限的整除关系中, 极小元是每一个质数; 没有极大元素.
有了类似于大于号的内容, 我们很自然的就会希望思考有没有类似于大于的内容. 这其实就是一个严格偏序关系(strict partial order).
3.8.11 (严格偏序关系). 令≺⊆X ×X是X上的二元关系, 如果满足≺满足下列条件, 我们说≺是X上的偏序关系.
(1) ≺是反自反(irreflexive)的: ∀x.¬(x ≺x);
(2) ≺是非对称(asymmetric)的: ∀x,y ∈X.x ≺y →¬(y →x);
(3) ≺是传递(transitive)的: ∀x,y,z ∈X.x ≺y ∧y ≺z →x ≺z.
这样的例子包含如我们探讨的整数上面的小于和大于; 以及集合和真包含于的关系.
事实上, 这个的第二个内容是不完备的, 这个内容可以通过第一条和第三条组成.
下面我们来看另一种全序关系. 全序关系可以认为是偏序关系+连接性–任意的两个元素都是可以比较的.
(1)自反的(∀x ∈X,x ≼x);
(2)对称的(∀x,y ∈X,x ≼y ∧y ≼x →x = y);
(3)传递的(∀x,y,z ∈X.x ≼y ∧y ≼z →x ≼z), 就称作R是A上的偏序关系. 通常记为≼. 整个序关系可以写作(X,≼);
(4) 连接性(connex): ∀x,y ∈X.x ≼y ∧y ≼x.
同样的, 我们也有严格全序关系:
3.8.13 (严格全序关系). 令≺⊆X ×X是X上的二元关系, 如果满足≺满足下列条件, 我们说≺是X上的严格全序关系.
(1) ≺是反自反(irreflexive)的: ∀x.¬(x ≺x);
(2) ≺是传递(transitive)的: ∀x,y,z ∈X.x ≺y ∧y ≺z →x ≺z.
(3) 半连接性(semi-connex): ∀x,y ∈X.(̸x = y) →x ≼y ∧y ≼x.
这样子(ℝ,<),(ℝ,>)的内容就是这样的例子.
我们在前面的数学归纳法一节中, 我们已经接触到了这样的一种性质. 下面, 我们再来看看有什么的应用.
我们发现, (ℕ,≤)是, 但是(ℤ,≤), (ℝ,≤)不是. 我们发现, 我们总是在一个全序集上面做–比如, ℤ上或者ℤ的一部分. 那么, 我们会想所有的良序集是不是一定是全序集呢? 其实答案是是的.
要说明这个定理, 我们需要考虑任意的两个元素x,y ∈X, 考虑{x,y}非空子集. 我们发现x ≼y,y ≼x, 这样就就是全序集了.
我们在高中的学习中, 对于极限的了解仅仅停留在表面和直观感受上. 那么, 我们有没有办法把这件事情严格化呢? 这是我们这次主要需要的事情.
From his paradise that Cantor with us unfolded, we hold our breath in awe; knowing, we shall not be expelled.
— David Hilbert
在《几何原本》中, Euclid明确提出: “整体大于部分”的公理. 但我们对无穷多个元素的集合而言, 部分是可以“等于”整体的.
考虑下面的两个集合:
我们可以给S1的每一个S1中的元素a做映射a2, 使得a2 ∈A
2, 因此可以认为这是相等的. 但是明显的, S2 ⊆S1. 这就是所说的“部分等于全体”.
用我们有限的心智来讨论无限
“说到底‘等于’、‘大于’和‘小于’诸性质不能用于无限而只能用于有限的数量。” — Galileo Galilei
当时也有人反对使用“无穷”的论点, 认为这是一派胡言.
“无穷数是不可能的。” — Gottfried Wilhelm Leibniz
但是Cantor坚定地认为, 以前我们的“大于”, “小于”那一套东西已经过时了, 要讨论“无穷”, 当然要建立一套新的体系, 来帮助我们理解这一套内容.
“这些证明一开始就期望那些数要具有有穷数的一切性质 或者甚至于把有穷数的性质强加于无穷。
相反这些无穷数如果它们能够以任何形式被理解的话 倒是由于它们与有穷数的对应它们必须具有完全新的数量特征。
这些性质完全依赖于事物的本性
而并非来自我们的主观任意性 或我们的偏见。”
— Georg Cantor (1885)
于是他们尝试使用映射的观念来定义无穷:
3.9.1 (Dedekind-infinite & Dedekind-finite (Dedekind, 1888)). A set A is Dedekind-infinite if there is a bijective function from A to some proper subset B of A.
A set is Dedekind-finite if it is not Dedekind-infinite.
但是我们还没有定义“finite”和“infinite”. 所以下面我们要用函数的观念来比较集合.
从开始的问题中, 我们可以看到, 只要出现了一个双射函数, 我们就可以说两个集合的元素个数相等. 于是给出如下定义:
3.10.1 (|A|= |B|(A ≈B) (1878)). A and B are equipotent (等势) if there exists a bijection from A to B.
一个集合其实是不关心这个集合元素的次序,在“势”的考量下, 也不关心集合中的元素是什么, 就是两层抽象. 有时候也写作A.
那么, 等势关系是一个等价关系吗? 不要关注太多, 要想证明远没有想象的那么简单.
3.10.1. The “Equivalence Concept” of Equipotent For any sets A, B, C:
有了“势”的概念, 我们就可以对“有限”进行定义了.
我们很多时候写作|X|= n. 这就意味着集合 X 是有穷的当且仅当它与某个自然数等势.
相反的, 我们可以定义无穷.
我们既然定义了, 当然要说明它是存在的. 于是我们有这样的一个定理:
我们可以使用反证法证明.
. 假设∃n ∈ℕ, 使得|ℕ|= n, 那么我们就存在f : ℕ 1−1
←− →
onto {0,1,,n −1}.
下面, 我们构造限制映射g ≜ f|{0,1,…,n} : {0,1,,n} → {0,1,
,n − 1}. 由于抽屉原理, g不是一一映射,
那么f也不是一一映射.
□
我们注意到无穷也有几种. 比如有的无穷是可以一个一个计数清楚的, 有的无穷是不行的.
自然的, 我们会发现ℤ是可数的. 如果我们把ℕ的每一个元素扩大到原来了2倍, 中间就会稀疏一些, 可以容纳下负数.
Cantor发现ℚ也是可数的. 因为Cantor是发现了一种数出有理数的方法. 其一句就是任何一个有理数(quotient)都可以成为形如a∕b,gcd(a,b) = 1成比例的数. 如此:
因此, 有理数是可数的. 更进一步的, ℕ ×ℕ也是可数的. 因为我们只要做一个映射就行了. 具体的, 可以把ℕ ×ℕ压缩到ℕ上.
也就是π(k1,k2) = (k1 + k2)(k1 + k2 + 1) + k2.
按照归纳的方法, 也就是π(n)(k 1,…,kn−1,kn) = π(π(n−1)(k 1,…,kn−1),kn) (n ≥3), 有如下的定理:
进一步的推广, 我们有:
另外, 任意有限集的并集都是可数的, 我们还可以用刚刚的想法, 使用对角线计数.
再后来的研究中, 我们惊奇的发现, 有些无穷的大小之间是有着深刻的差别的. 例如, ℝ是不能够被数出来的. 同样也是用对角线证明法得到的结论.
这个定理就告诉我们了实数不能被表示成有理数的有序对. 这就说明了ℝ是一个连续统. 另外一个惊人的事情是, (0,1)之间的实数和ℝ, ℝ ×ℝ的势是一致的.
一个可能的证明方式是考虑
但是很不幸, 这个证明是错误的. 严格的证明需要系统地学习数学分析才可以知道.
在成功证明这件事情之后, Cantor写给Dedekind的一封信里面说到: “Je le vois, mais je ne le crois pas !” 翻译成英语就是“I see it, but I don’t believe it !”. 可见这样对于“无穷”的探讨是十分激动人心同时也是令人感到违背常识的.
更惨的还在后面: 我们在《线性代数》课程和之前的理解上, 维数好像总是有限的. 但是Cantor的论述让我们对于“维数”的理解出现了很多问题. 其中一个问题是, 我们能不能通过一个双射把m维的东西映射到n维去?
3.10.7 (Brouwer (Topological Invariance of Dimension)). There is no continuous bijections between ℝm and ℝn for m≠n.
什么是continuous的双射? 这个就需要更多数学专业的知识了. 在这里不做阐述了.
连续统假设说明的是
事实上, 这是一个没有办法证明的命题. 我们可以看Dangerous Knowledge来了解更多.
计算机系统中没有魔法. – 蒋炎岩
计算机的一个重要的功能是存储和操作数据. 那么从“数据”的角度看通过算法希望计算机帮我们解的“题”与你们中学数学课上解的题有什么不同
事实上, 算法的输入是满足特定条件的对象的集合“问题空间”算法必须能保证对该集合中“任一对象”均能计算出正确的结果。程序是算法的“实现”其“每一次”执行处理的是某个特定数据对象(问题实例)。
因此中学数学课中的那些“题目”是我们这里讨论的算法问题的“实例”。因为我们只需要对于单一的个体进行回答.
对于算法而言, 为什么讨论计算机问题求解必须讨论“数据”首先, 输入数据必须以某种形式“放入”计算机输出结果必须以某种形式的数据呈现给用户问题求解过程可以看作“数据转换”过程这个过程如果有多个步骤组成则每个步骤可能需要以中间形式暂时存放供后面的步骤使用。
最基本的数据可以说为变量了. 在第一章中, 我们说明了我们认为变量是存储一个“东西”的盒子. 我们说这个“盒子”其实有两种形式. 按值(by value)或者按引用(by reference). 见图.
比如, 在“冒泡”排序算法中核心操作是“交换序列中两个元素(不妨说是x,y)其实现过程可以表示如下注意需要使用一个临时辅助变量z
在C语言中, 为什么对变量要指定“类型”首先, 变量的类型表示了这些变量够执行什么样的“操作”(运算). 我们为什么要给变量起名字? 其实变量名的本质在于. 变常量名是计算机存储区地址的“抽象”. 编程时关注的“位置”与计算机内的物理地址无关.
在数据结构中, “结构”究竟是什么实际上, 控制结构与数据结构是计算机算法的两个侧面数据结构不仅仅是关乎数据“如何放”。
While control structures serve to tell the processor where it should be going, data structures, and the operations upon them, organize the data items in ways that enable it to do whatever it should do when it gets there.
比如, “全班同学排好队”是什么意思首先, 每人有了一个“位置”。然后, 其实这个“位置”是相对的。其实, 如果安排一种按照位置进行的“游戏”“到了什么位置就知道该做什么”。
这样我们就知道了程序设计语言中的数组到底是什么. 数组就相当于抽象的逻辑结构是“顺序”结构. 在计算机中的“实现”就是同类型数据的“序列”。程序设计语言为你提供了定义特定数组的“设施”. 物理位置就可以不用管了.
我们选取的数据结构与控制结构的对应(图4.1). 来看几个例子.
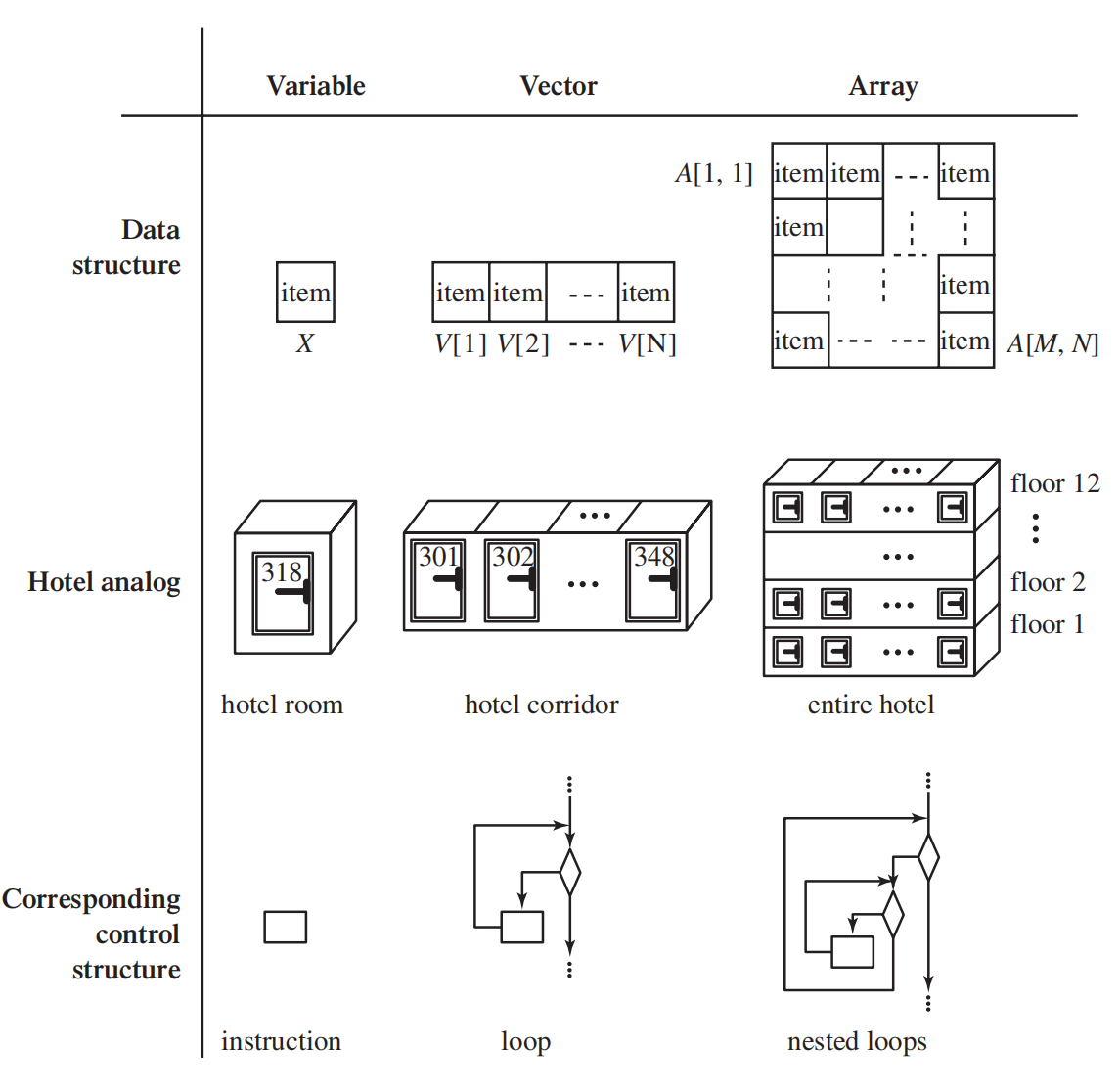
比如, 我们写了一个n维的数组, 但是可能想过, 数组维数的相对性. 比如一个二维数组可以写称为vector套vector.
这就是数组的一些有趣的事情. 下面来总结一下. 数组结构的访问方式特点是什么对于解题有什么好处又带来什么不便
数组元素使用“下标”确定其位置而下标是顺序编排的这对访问数组元素带来什么便利正因为顺序编排对于在应用中如果需要增删元素则必须“维护”相应的特性
你若需要对数组元素进行如下操作可能必须移动“整块”的其它元素(1)在指定位置插入一个新元素(2)删除某个位置上的元素但不留下“空挡”, 那么代价可能很大.
数组实际上是通过连续编排下标将元素顺序连接成一个“结构”. 如果我们将“顺序连接”抽象为对用户“透明”的实现方式那么数组就可以认为是“抽象数据类型”list的一种实现。list中“顺序”的概念是抽象的可以用不同方式实现. 常用的linked-list可以认为是一种使用“指针”的实现。显然linked-list(链表)可以解决数组的不便。而且更适用于执行前无法确定序列长度的情况。
我们发现我们不关心这里面的数据到底是什么. 所谓“抽象数据类型”不涉及数据对象的性质以及其“存放”方式仅通过操作定义体现在“解题”时的应用意义。比如, 简化的list由4个操作定义(1)一个创建(插入)操作两个“查询”操作一个常量.
1list cons(obj newElement, oldList) 2Precondition: none 3Postcondition: if x=con(newElement, oldList) then: 4 (1) x refer to a newly created list 5 (2) x!=nil 6 (3) first(x)=newElement 7 (4) rest(x)=oldList 8obj first(list aList) 9Precondition: aList!=nil 10 11list rest(list aList) 12Precondition: sList!=nil 13 14list nil
我们来考察如下的两个情形: (1)在图书馆的书架某一层取一本书; (2) 在机场的饮水机旁取一个纸杯. 这两者有何不同其实, 如果仅仅从“放置”的角度看两者涉及的物体放置方式是一样的“一个挨着一个的顺序结构”不同的是对元素的操作方式。我们的操作方式是被受到限制的. 即使一样的“受限”操作方式也可以有不同的“限”法比如栈(stack)和队列(queue)在不同的问题的求解有不同的明显的意义。
比如判定输入字符串是否“回文(palindrome)”也就是从头读到尾与从尾读到头完全一样. 一个最朴素的想法就是通过数组的方式存储每一个字符, 然后正着倒着循环并且判断即可. 另一个例子是模拟一个排队的场景: 设想一个单服务柜台的运行状态设定模拟总时间长度随机生成“新顾客到达时间及其需要的服务处理时长”模拟可能的排队等待队列人数变化情况。假设服务能力与预期顾客需求量总量平衡。既然是“队列”, 我们就不允许新元素“插队”了.
想一想大学里面选修课程的依赖, 以及家谱(family tree), 它们一般构成一个树的关系–这样非线性的内容是如何存在计算机中的呢? 事实上, 我们并不是真正的在内存里按照图形的样子进行存储的. 我们是使用引用的方式来把这个关系搞清楚的. 树的一个比较明显的特征是可分“层”.
我们在内存里面是如何存储树的呢? 事实上, 我们只要在每个节点上打上它儿子节点的编号就行了. 这样我们在找子树的时候就可以按照编号去对应的位置去寻找了. 当然这只是一种方法, 其他的方法大同小异, 不过这样一个对应关系还是绕不过去的.
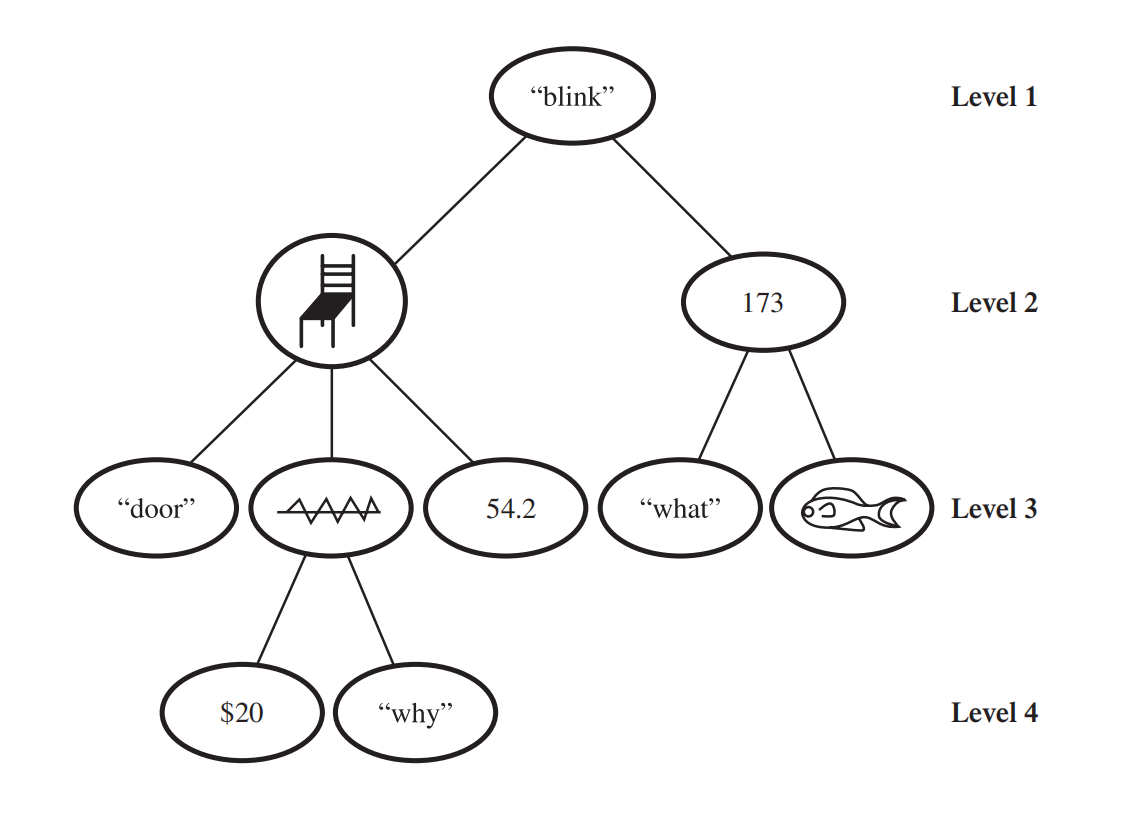
如果这里是一个数组或者嵌套的数组, 我们可以很容易的看到它里面的所有的元素是什么. 那么如果是树我们应该如何看到它的内容呢?
这就要回到我们如何看树了. 从非递归的视角来看, 我们有一个“结点”的集合{A,B,,K}, 以及一个“独特”的结点 – “根”A. 根只有“出边”没有“入边”.
其它任何结点有恰好一个“入边”, 这也就保证了每一个节点具有唯一的通路. 从递归视角来看, 会发现它有一个唯一的“根”结点. 假设根结点有k条出边其另一端点为
v1,v2,
,vk它们分别是k个无结点相交的树的根这些树称为“子树”.
从递归的视角来看树可以由很多的好处. 比如, 这就可以让我们发现如果要遍历一棵树, 那么先遍历左边子树, 在遍历右边的子树就行了. 这看上去比较抽象, 我们下面说几个比较有趣的例子.
例子1. 利用树排序. (见图4.3) 首先, 将数组表示为“二分搜索树”. “二分搜索树”的生成方式是这样的: 每个节点的左边节点的数值一定比它的值小, 右边的一定比它的值大. 以“深度优先”方式遍历树, 那么输出方式一定是从小到大的.
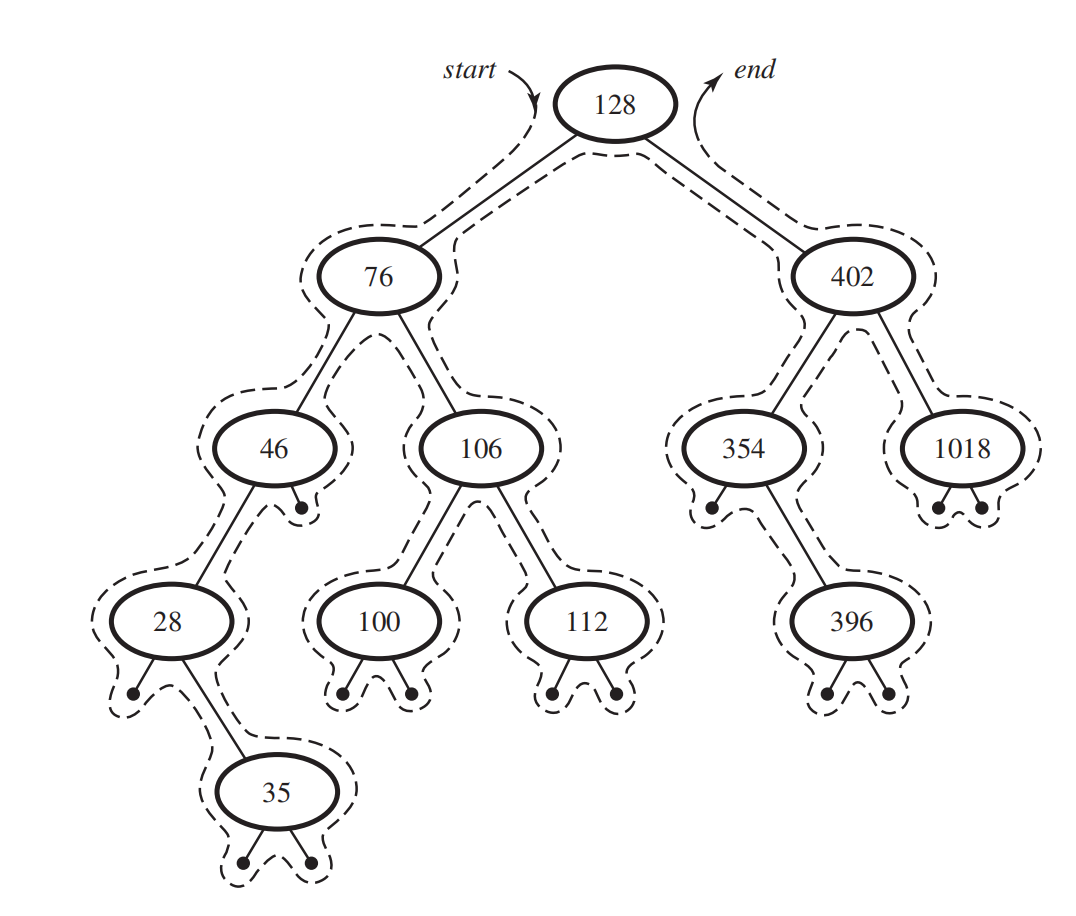
例子2. 树结构和算数表达求值. (见图4.4) 如算术表达式(10 + ((22–3 ×4)∕2–2 ×2) ×((14–2)∕(1 + 3)). 对应的表达式树就是这样的:
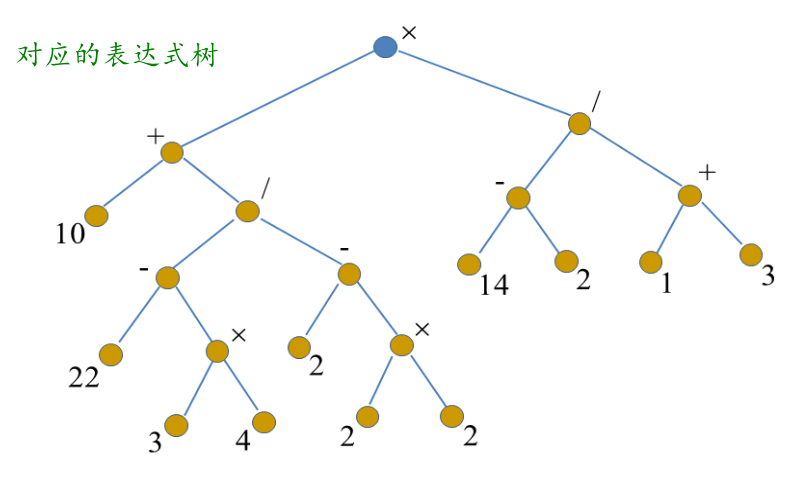
我们使用Left-first traversal(Third-visit output, 称为“后序”).
其实还有一个新的方法: 假如数字输出到一个堆栈中每当遇到运算符则处理前面两个数结果仍然是对的.
我们可能会说, 把算法告诉计算机有什么难的? 写点代码就行了啊! 但计算机的最底层是01的组合, 我们今天并没有用0,1表述我们的算法.
事实上, “早期”的程序员真的用0, 1编程序. 他们使用的是打孔纸带和操作系统进行. 其一般有三个部分组成. 如图4.5. 就是一条条这样的“指令”用来告诉物理的电路要做什么: 哪个开关打开, 哪个应该关闭. 计算机虽然能接受这样的语言表述但并不知道你究竟“想干什么”–因为“编程自动化”远比“算法设计自动化”要容易!

与程序对应的, 就是把“程序”放入计算机的存储里面的Von Neumann的体系结构. 相比于以前每一次写一个新程序就要重新去接线来说, 这样的内容确实简化了不少. Von Neumann构想的“计算机”应该由这四个内容组成: 内存(memory); 中央处理器(central processing unit): 其中包括控制单元(contol unit)和算术逻辑单元(arithematic logical unit, ALU), 分别控制按照规定的顺序执行以及计算其中可能的表达式; 以及输入输出设备(input/output devices).

我们的计算机科学家很快就发现了这件事情很难办, 因为首先, 这一堆东西根本难以阅读. 聪明的计算机科学家采取了把那些抽象的数字和指令编号用一个一个比较直观的简单的记号, 这样一来就至少不会让我们感到头晕眼花了. 但是, 我们还是不知道这个程序到底要干什么. 比如我们要实现对输入的非负整数进行累加遇到负数停止这样一个简单的操作, 我们可能需要写这样的程序, 见图4.6.
这就是我们为什么要使用高级的语言了. 由于项目变大的时候这些内容根本难以维护, 这就爆发了“软件危机”–越想改好, 但是bug越来越多.
The major cause of the software crisis is that the machines have become several orders of magnitude more powerful! To put it quite bluntly: as long as there were no machines, programming was no problem at all; when we had a few weak computers, programming became a mild problem, and now we have gigantic computers, programming has become an equally gigantic problem.
–Edsger Dijkstra, The Humble Programmer (EWD340), Communications of the ACM
人们感到十分的苦恼. 有没有一个更抽象的东西让我们把这些都机械化地管好呢? 其实是有的, 打败powerful computer的最好的办法就是设计一套规则, 让我们自动的管好这些我们不想理睬的power.
我们期望的编程语言应该什么样? 相较于汇编语言直接与机器像婆婆妈妈那样事无巨细的吩咐好, 我们不妨想创建一个小管家, 让它可以帮助我们做得更加抽象一点, 比如:
程序员不需要关心数据究竟放在那里也不必理会数据在存储器中的移动的细节;
下面我们来看一下从数据到算法, 我们经历了什么:
一个非常直观的思想是: “逐个”检查每个元素是0就删除。但如果从“思想”到“算法”的话, 还需要回答:
回答了这个问题, 我们可以提出“Converging-Pointer算法” 采用两个“指针”从序列两端相向移动左指针管“检查”右指针管“填空”当两指针相遇时就到算法该结束的时候了。
好, 有了这个思想, 我们就可以写出如下的伪代码:
输入正整数
1n // 是待清洗数据序列长度n数组 2data输入序列:= 3legit:=n // 有效数字计数器赋初值legitn 4left:=0 // 当前检查位置指针赋初值left0 5right:=n-1 // 当前序列末位置指针赋初值rightn-1 6while not(left>right) do 最后一次循环//left=right 7 if data[left]=0 then 8 legit:=legit-1 9 data[left]:=data[right] 10 right:=right-1 11 else 12 left:=left+1
然后就可以写出C++的代码了.
1while (left<right){ 2 if (data[left]!=0) 3 left=left+1; 4 else{ 5 legit=legit-1; 6 data[left]=data[right]; 7 right=right-1; 8 } 9} 10if (data[left]==0) legit=legit-1; 11
我们来看一下这份讲义, 我们日常生活中主要的语言: 汉语. 我们在高中的时候可能会了解: 这些句子的组成结构组成的汉语句子是符合语法的.
句子
1<>主语动宾结构 2<><>主语谓语宾语 3<><<><>>主语谓语 4<><>主语状语谓语 5<><><>主语谓语补语 6<><><>名词副词动词名词 7<><><><>名词动词补语 8<><><>王同学动宾结构 9<>王同学学习名词 10<>王同学状语学习数学 11<>王同学副词学习数学 12<>王同学努力地学习数学。
如果有的句子与没有出现在语法中, 如“王同学努力地数学学习”, 我们就可以认为这是语病, 写在作文里是要扣分的. 但是还有一类句子, 如“数学努力地学习王同学”, 虽然合乎语法, 但是并没有道理. 我们说这个矩阵不是“合理”的. 我们为什么会这么说? 因为我们关注了一个语言的两个重要的部分: 语法和语义(就像在第一章提到的一样). 既然两个都叫做“语言”, 那么他们的相似之处也不少, 程序设计语言和自然语言最大的不同在哪里
其实, 程序设计语言是人专门“设计”出来的. 比如C++之父Bjarne Stroustrup, Java之父James Gosling. 目前, 维基百科上已经提到了有超过700种程序语言.
要设计程序设计语言, 要拿出的心思更多应该在权衡上. 为什么这样说? 我们应该权衡什么? 首先要观察机器“能”或“不能”; 齐次要观察人类是不是方便. 作为一个机器, 其只是没有感情的工具, 因此我们必须要求语言完全没有歧义, 并且解释的规则是完全确定的. 什么是“规则”? 比如语言定义的两个要素语法(什么样的形式是“合法”的)和语义(合法的形式是什么意思(例如执行后会产生什么效果))的精确定义1 . 正是这样严苛的规则, 保证了“机器永远是对的”.
两个人用自然语言沟通两个人都可能在语言使用上“出错”但人和机器沟通“出错”的一定是人。
我们所谓的语言, 一般都是由句子构成的. 为了简化我们的探讨的深度, 这里我们先只考虑“形式语言”–即只有“句子”组成规则但“句子”没有“含义”的语言. 我们可以从如下的几个方面来说明:
再规定哪些“用a,b构成的符号串”是语言L中“合法”的句子. 这些被称为生成规则.
用更加正式的内容来描述我们刚刚的内容, 我们就可以写成L = {w|w = aa∗bb∗}. 这样的表达形式叫做正则表达式(regular expression). (这个内容表达的意思就是至少1个a后面接至少1个ba,b数量可以是任意正整数)
现在, 我们可以有正则表达式来定义语言. 正则表达式的语言定义如下:
4.2.1 (正则表达式语言的定义). 假设字母表 Σ = a,b, 定义 Σ 上的正则表达式如下
其中αβ表示把α,β两个表达式并列放置; α ∨β表示α,β的任意一个出现; (α)∗表示α出现零次或者任意有限多次.
现在有这样的一个问题: 如果让你用C语言, 输入一个规则和一系列字符串, 那么你能不能给出这个字符串“满不满足”这个规则呢? 对于这个内容的探索, 激发出了有限状态自动机(deterministic finite-state automation)的探讨. 一般来讲, 它由以下的几部分构成:
上面问题的内容画出来就像是图4.7

但是随着时间的发展, 我们发现用正则表达式能定义的表达力有限下面的语言就无法用正则表达式描述
于是我们聪明的计算机科学家们发明了短语结构文法(phrase-structure grammar), 定义为四元组: G = (V,T,S,P):
4.2.2 (短语结构文法). 短语结构文法 (phrase-structure grammar) 定义为四元组 G = (V,T,S,P):
确定一个句子的过程叫做“derivation”. 比如图4.9
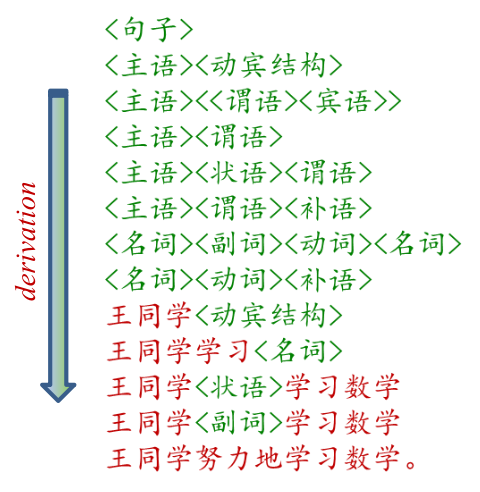
正则表达式对应着正则文法, 但是这个内容没有办法满足我们对于我们希望表达的东西的需要. 于是我们发明了“上下文无关文法”. 上下文无关文法的一个特征是所有的生成式的左侧只有一个非终结符. 一些关键词的语法定义可以参见??.
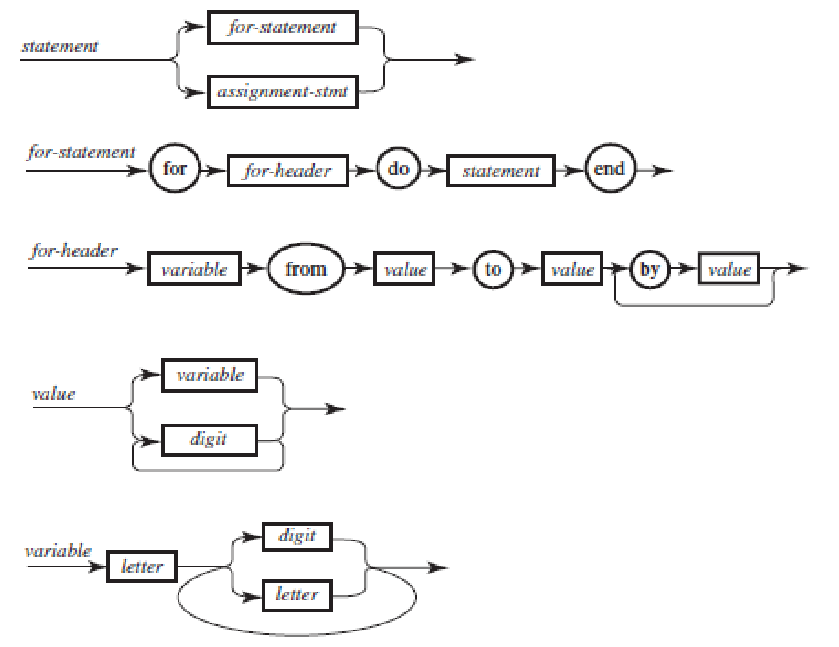
相应的, 我们也有相应的Bachus-Naur范式表述这些图片.
1<statement>::=<for-statement> | <assignment-statement> 2<for-statement>::= for <for-header> do <statement> end 3<for-header>::=<variable> from <value> to <value> (by <value> | <empty>) 4...
如果大家看过Python文档比较深刻的地方, 相信这些都是老面孔了!
好了, 这就是我们计算机科学家们对于程序“语法”的意思了. 更多的内容可能就要在编译原理这门课中继续讲解了.
𝔹onus
想知道你的C编译器是如何编译你的代码的吗? 欢迎收看魏恒峰老师开讲的《编译原理》! 在 https://www.bilibili.com/video/BV1Bs4y187kK这里找到今年(2023年)的录屏.
至于“语义”是什么, 就更加难以在这里说清楚了. 随便的几个问题可能就非常的深刻. 比如:
这就说明, 能够提供一套“规则”使得人和机器对于用程序设计语言表述的内容不仅是形式有较高的共识这远比定义文法困难。
不管采用什么文法、语义目前我们都不能让计算机直接听懂你要它干什么那你的程序是怎么运行的呢这就是编译器的工作了. 我们目前能做到的就只有把要写的代码写好, 在前人的心血上, 程序才能让电脑“听懂”(如图4.10). 之所以我们还可能用自然语言描述程序设计语言的语义那是因为“说”的对象还是人而不是机器。
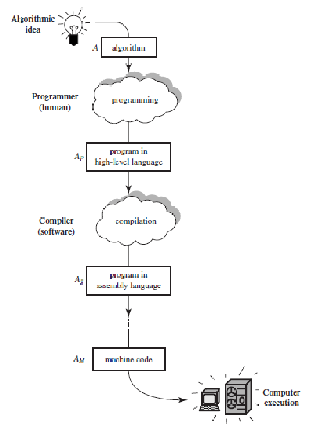
计算机永远是对的! – 蒋炎岩, 余子豪等
计算机是人造的科学, 因此, 很多的情形就是我们的错误 – 有可能是你的情况, 也有可能是参与建设更加基本抽象层的人的问题.
𝔹onus
我们经常发生错误的愿意是什么?
问题求解: 第二部分
这一部分是问题求解课程讲义的第二部分. 我们会讨论更多有趣的问题. 当然, 我们会遇到更多具有挑战性的问题. 我们一起来攻克它们!
这一部分, 我们希望可以理解解数据抽象理解并能够应用常用的数据结构; 掌握重要算法设计策略以及算法设计与分析的基本方法以及理解并能够应用支持上述内容的离散数学工具与方法. 祝大家好运!
我们都是活生生的人, 从小就被不由自主地教导用最小的付出获得最大的得到, 经常会忘记我们究竟要的是什么. 我承认我完美主义, 但我想每个人心中都有那一份求知的渴望和对真理的向往, “大学"的灵魂也就在于超越世俗, 超越时代的纯真和理想 – 我们不是要讨好企业的毕业生, 而是要寻找改变世界的力量. – 蒋炎岩