4LN - 函数: 我们需要更深入些

回答一些疑问

• 为什么上节课程没有总结?
  • 好问题, 不过确实是我忘了...
  • 还有一个原因是, 我希望你自己可以有这个意识.
  • 但显然两三次的总结给你看, 样本有点太少了.
  • 所以以后, 我们恢复这个惯例.
  • 这次就两节课合并起来吧!

接着说函数的三要素

定义域

• 定义域不同, 就一定是不同的函数.
• 题目会让我们求定义域.
  • "只需周官放火, 不许百姓点灯"
  • 考试的时候不写定义域是为了考你.
    • 偶数次根号下非负
    • 分母不为0
    • (还没学)真数大于0
    • $0^0$无意义.

看Ex1.全部和Ex2.

• Prob1-5. 一层一层看! $x<0 \text{ and }x\neq 1/2$.

值域

• 简单的函数: 一次函数, 二次函数, 反比例函数.
• 反比例函数: $y=1/x$, ${y| y\neq 0}$, ${x| x\neq 0}$ 对吗? 对! 因为代表元素是核心. (但是别扭).
  • $y=1/x+1=(x+1)/x$
  • 显然, 后面的看上去费劲. 所以考试题会这样出:

例子: 求值域$y=(2x+3)/(x-1)$.

• 方向: 放回去, 就成了$2+5/(x-1)$. ($y\neq 2$)

• 这叫分离常数(dissociation constant(s)).

• 原理: 考虑平移. 先向右平移, 乘5倍, 再向上平移. 例子: 求值域$y=(3x-1)/(2x+1)$.

• 为啥非得分离? 答案不是写在式子上吗?

  • 推导一下一次比一次的.

例子2: $$ y={x^2+4x-5\over x^2+3x-2}. $$

• 来个因式分解. 得到$y\neq 1$
• 戳啦! 定义域不同! $x\neq 2 并且 x\neq 1$, 带回去, $y\neq 1并且y\neq 6$.

求值域将会贯穿整个高中, 不止这些!

映射

函数和映射有什么区别?

定义(映射): 一般地，设,$A,B$ 是两个非空的集合，如果按某一个确定的对应关系$f$ ，使对$A$ 中的任意一个元素$x$ ，在集合$B$ 中都有唯一确定的元素$y$ 与之对应，那么就称对应$f$ 集合 $A$ 到集合 $B$ 的映射．映射 $f$ 也可记为为$f:A\to B$. (复制粘贴的, 供找不同使用).

定义(函数): 对于非空数集$A,B$, 存在对应法则, $f: A\to B$.对于$\forall x\in A$, 在$B$中存在唯一确定的$y$与之对应.写作$y=f(x)$. 成$f$是定义在$A$上的函数.(复制粘贴的, 供找不同使用).

具体而言: 函数是特殊的映射(数到数的映射). 一些概念: 象(image)(中箭), 原象(preimage)(放箭) 那么, A集合的每个元素都是原象吗? B集合的每个元素都是原象吗?

分类: 一些战法

• 单射: 每个象只有一个原象. (每个人只中一箭). $|A|\leq |B|$.

• 满射: 每个B中元素都是象. $|A|\geq |B|$.

• 双射: (一一映射), 单射+满射.$|A|=|B|$.

  • 两个方向都可以寄信. (可以回信). 反函数(inverse function; )(留个悬念).

• 看3.(1)(2)(3)

数(3声)映射

$A=[a,b]; B=[c,d]$ 4个.

$A=[a_1,a_2,\cdots,a_m], B=A=[b_1,b_2,\cdots,b_n]$, 一共有$n\times n\times \cdots\times n = n^m$.

• 看Ex4.

复合函数: 拥有一切的开始

你有没有好奇过

• 牛变成罐头?
  • 拆开, 一步一步变化.
• $牛\rightarrow 取肉(牛) \rightarrow 腌制(取肉(牛))$
• 函数也有类似的操作.
• 什么是函数的复合? 先$f$一下, 再$g$一下.

函数的复合(composition): 对应法则

• 概念: 内层, 外层, 整体.
• 有时候也会用$\circ$表示复合的过程.
  • $g(f(x))=g\circ f$. (从右往左读的).
• 解析式
  • $f(x)=x+1, g(x)=x^2+1.$
  • $g(f(x)), f(g(x))$试试看.
  • 好像找爸爸, 找妈妈是两个函数, 找妈妈的爸爸$\neq$找爸爸的妈妈
  • 看Ex5(1). 注意定义域.你扔0, 第一步就不行了
  • Ex5(2).
  • Ex5(3).
  • $(2x+1)/(x+1), (5x+3)/(3x+2), (13x+8)/(8x+5)$

看6.

• (1) 换元而不是还原! 注意: 定义域, $u$的范围是什么?

函数的复合: 定义域(contd)

• 一个误解:

  • 如果$f(x)$定义域$(1,3)$, 那么$f(x+2)$定义域是.
  • $(3,5)$是错误的.
  • "骑驴找驴", 回到圈圈图上.(放箭的那些人)
  • 应该是$(-1,1)$

• 更多练习: 如果$f(x+2)$定义域$(1,3)$, 那么$f(2x-1)$定义域是$(2,3)$. 更简洁的方法: 用虚线隔开.

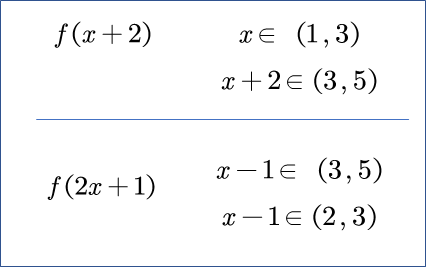
• 三句话:

  • 不同的函数, 不同的自变量.
  • 定义域: $x$的范围.
  • 都不一样怎么算? $x$的所用范围相同.

• 看7(1)(2). 要前后两个函数的交集

复合函数: 值域

• 原则: 由内往外, 一层一层.

$$ p(h(g(f(x)))) $$

• 看8. 答案: $y\in (-\infty,3)\cup[4,+\infty)$

• 一次, 二次, 反比例, 开根号的复合.

• 看10(1). $a\geq 2/3$, 没说在别的地方没意义.

• (2)

• (3) $a>0, Δ≥0$ 或者 $a=0$, 解答$[0,1]$.

函数: 共同之处

上升, 下降? ... "升降性"? "单调性". 升的快, 升的慢?... "折性"? "凹凸性". 这些共同之处叫做函数的性质.

小球在函数图像上有时候滚, 有时候不滚... "滚性"? 驻点 无限放大, 就可以化曲为直...

对称性. 按照轴, 中心, 一条直线对称?... (逐)渐(在接)近(的)线...

我们在下一节先了解: 单调, 对称性...

总结: 学到了什么

复杂的东西总是存在简单的解释

• 比如通过复合, 我们就可以瞬间得到一个极其复杂的东西.
• 然而这是任何一个复杂系统的最佳阐释.
  • 举个例子, 计算机
  • 航空母舰
  • ...

函数

• 重点就是三要素, 以及它们的一些操作.
• 复合是一个非常有意思的操作.
• 课下探讨11.
• 下面我们将入手一些性质, 还要认识一下新函数(基本初等函数(basic elementary functions))

2话以来, 有悬念吗?

• 反函数.
• 容斥原理. 参考书目: 《组合数学》第六章.

科技的力量: 如何用计算机画函数图像.

不要滥用! 例如在考试的时候使用. 仅供平时探索的时候使用.

教育除了知识的记忆之外, 更本质的是能力的训练, 即所谓的training. 而但凡training就必须克服一定的难度, 否则你就是在做重复劳动, 能力也不会有改变. 如果遇到难度就选择退缩, 或者让别人来替你克服本该由你自己克服的难度, 等于是自动放弃了获得training的机会, 而这其实是大学专业教育最宝贵的部分. -- etone, NJU

Geogebra

End

Good luck and have fun

高中之后, 是大学.

我们都是活生生的人, 从小就被不由自主地教导用最小的付出获得最大的得到, 经常会忘记我们究竟要的是什么. 我承认我完美主义, 但我想每个人心中都有那一份求知的渴望和对真理的向往, "大学"的灵魂也就在于超越世俗, 超越时代的纯真和理想 -- 我们不是要讨好企业的毕业生, 而是要寻找改变世界的力量. -- jyy(蒋炎岩), NJU