5LN - 函数的性质(property)

先聊点闲话

• 我们问了好多问题是吧!
• 好多问题可能没人有功夫解答/不愿意解答
• 好多时候那我们可以找计算机来帮助

电脑的力量

引言

• 众所周知, 我们从小就被限制打游戏, 最近国家也限制我们打游戏了.
• 我的评价是: a fxxking bullsxxt.
• 可能是由于这些限制吧, 我们的"玩电脑能力"真的是一代不如一代.
• 但是作为一个现代人, 你必须会"玩电脑".
• 比如, 上网查找一些资料, 与同学交流等等.
• 在这个小节, 你将会学到
  • 如何正确(意思是: 高效, 有用)地搜索;
  • 如何正确在Geogebra中输入你想绘制的函数曲线;
  • 如何提问.
• 以我的经验来看, 足够好的资料都在互联网上. 讲义上没必要出现这些内容的具体实现.(当然我会给你演示的!)

有了互联网, 你可以学习任何知识!

学习(术)诚信(Academic integrity)

• 有了互联网, 也让抄袭(plagiarism)悄悄生根.
• 高考过分强化训练, 并不关心你们(部分)扭曲的价值观.
• 所以很多人到了大学之后就...

• ...放飞自我了(详见代码抄袭).

我们现在所处的模式: 被告知要最大化分数, 来得到所谓理想的结果.

为什么要这样做? 他们说的真的可信吗?

我们都是活生生的人, 从小就被不由自主地教导用最小的付出获得最大的得到, 经常会忘记我们究竟要的是什么. 我承认我完美主义, 但我想每个人心中都有那一份求知的渴望和对真理的向往, "大学"的灵魂也就在于超越世俗, 超越时代的纯真和理想 -- 我们不是要讨好企业的毕业生, 而是要寻找改变世界的力量.

大家一定有一个共识: 提升能力是硬本事.

基于此, 大家就有了实行学习(术)诚信的前提条件.

学习(术)诚信

• Academic integrity 不是底线，而是 “自发的要求”
• 对 “不应该做的事情” 有清楚的认识
  • 不自欺欺人, 坦诚面对自己的错误
  • 平时考试练习不抄别人的答案
  • 不糊弄习题.
• 有些行为可能使你得到暂时的分数(和心理的安慰)，但失去应有的训练.
• 只在 “绝对可以求助” 的时候才寻求帮助(良心不会痛)
  • 在全民内卷、作业繁多的时代很难
  • 但坚持下来的人会变得很不一样

蒋炎岩语录:

大家在这个全民内卷, 不劳而获的时代, 但是想要坚持这一点(学术诚信)还是有一点难的. 但我觉得如果你能坚持下来, 你就能变成一个很不一样的人.

困难的东西总是存在简单的解释. 简单, 意味着用正确的或者专业的视角把整个学科的知识体系构建起来, 简单, 恰恰意味着专业的训练和痛苦的折磨. 然后我就会提到那句话说"Real power cant be given, it must be taken", 我们试图给你们的只是我们的一厢情愿, 你们要在你们的programatic里面体会我们的用心. 你们要去'take'他, 就像我今天讲的, 你们就take了这个想法, 这就有点不一样了.

一个例子: 平时挺好, 考试不行?

• 正确率/时间要求不严格.
  • 在全民内卷、作业繁多的时代很难
  • 但坚持下来的人会变得很不一样

函数的性质: 单调性(monotonicity)

转化为代数结构

转化成代数形式? 因为这是两个数的比较关系...

$f(x)$定义域$D$内一个区间$M$(不一定整体), $\forall x_1, x_2 \in M, x_1<x_2$. 若$f(x_1)<f(x_2)$, 称$f(x)$为区间$M$上的增函数. 若$f(x_1)>f(x_2)$, 称$f(x)$为区间$M$上的减函数. 统称为"有单调性".

注意

• 这是局部性质, 配合着区间来说.
• 严格的$>,<$.
• 有可能不增不减. $f(x)=1$, Dirichlet函数.
• 区间之间不能用并集.
  • 可以写"和".

例子:$f(x)=1/x$在定义域上是减函数? $f(x)=x^2$的单调性, 区间的开闭?

• 对连续的函数, 在端点处有定义, 开闭区间均可.
• 变形形式
  • $(x_1-x_2)(f(x_1)-f(x_2))>0$, 增函数.
  • $((f(x_1)-f(x_2))/(x_1-x_2))>0$, 增函数.

看Ex1.

• Trivial.

判定方法

• (1) 一次, 二次, 反比例: 想象图像.
• (2) 定义(格式要求):
  • $\forall x_1, x_2 \in \R, x_1<x_2$. (希望$f(x_1)-f(x_2)<0$, 比较经常做差)

因为$x_2$大, 所以$x_2^3$大, 所以证毕, 还挺轻松?

• 错啦!为什么$x_2^3$就大了? 这是循环论证啊!
• 老老实实分解因式, 看看发现什么.
  • 配方: 消灭交叉项.

$$ \begin{aligned} & f\left(x_{1}\right)-f\left(x_{2}\right) \\ =& x_{1}^{3}-x_{2}^{3} \\ =&\left(x_{1}-x_{2}\right)\left(x_{1}^{2}+x_{1} x_{2}+x_{2}^{2}\right) \\ =& \underbrace{\left(x_{1}-x_{2}\right)}{<0}[\underbrace{\left(x-\frac{x{2}}{2}\right)^{2}+\frac{3}{4} x_{2}^{2}]}_{\geq0} \end{aligned} $$

• 为什么不可能取得等号? 不都为0.

技能点: 因式分解, 配方.

$f(x)=x^3+x$的单调性?

• 如何说明$h(x)\nearrow=f(x)\nearrow+g(x)\nearrow$?

• (3) 函数的运算

$\nearrow+\nearrow=\nearrow$ $\searrow+\searrow=\searrow$ $\nearrow-\searrow=?$ $\searrow-\nearrow=?$

看Ex4. 正函数乘/除增函数? 找一点具体的函数试试, 再考虑一般.

• (4) 函数的复合
  • 本质: 自变量的变化和函数值的变化趋势是否相同.

单调性? 和内外层函数的关系有关系?

画圈圈图! (举个例子) 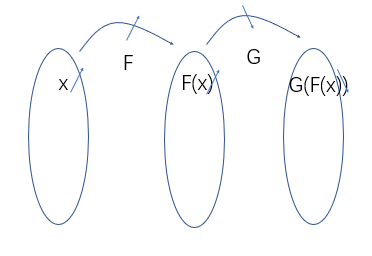经过探讨发现, 同增异减(两层复合), 不要死记, 后面有误导的可能!

三个呢? $p=(h\nearrow)\circ (g\searrow)\circ (f\searrow)$

• 减函数作为"变号器".

例子: $f(x)=\dfrac{1}{x^2+2x+2}$, 注意分类讨论之.

例子(分更多类Ver.): $f(x)=\dfrac{1}{x^2+2x+2}$, 注意分类讨论之.

例子(另一方向分更多类Ver.): $f(x)=x^2-1, g(x)=x^2, h(x)=g(f(x))=x^4-2x^2+1$. 单调区间是什么?

看Ex5.

专项研究: 绝对值函数(Absolute value function)

生成一下$f(x)=|x-a|$的函数图像($a$是常数)

• 翻折, 平移
• "距离"

生成一下$f(x)=|x-1|+|x-2|$的函数图像

• 分类讨论?
• 翻折? 晕
• 距离!

生成一下$f(x)=|x-1|+|x-2|+|x-3|$的函数图像

来个好玩的Ex6.

那么如果$f(x)=|2x-1|+|x-1|$呢?

• 距离? 有点麻烦
• 等于$2|x-(1/2)|+|x-1|$

转化成功! 叠了几层就相当于斜率是几!

那么如果$f(x)=|x-1|+|2x-1|+|3x-1|+|4x-1|+|5x-1|$, 取到最小值, $x$是几?

思考: $|x-1|-|x-2|$会怎样?

专项研究: 对勾函数(不正式的名字)

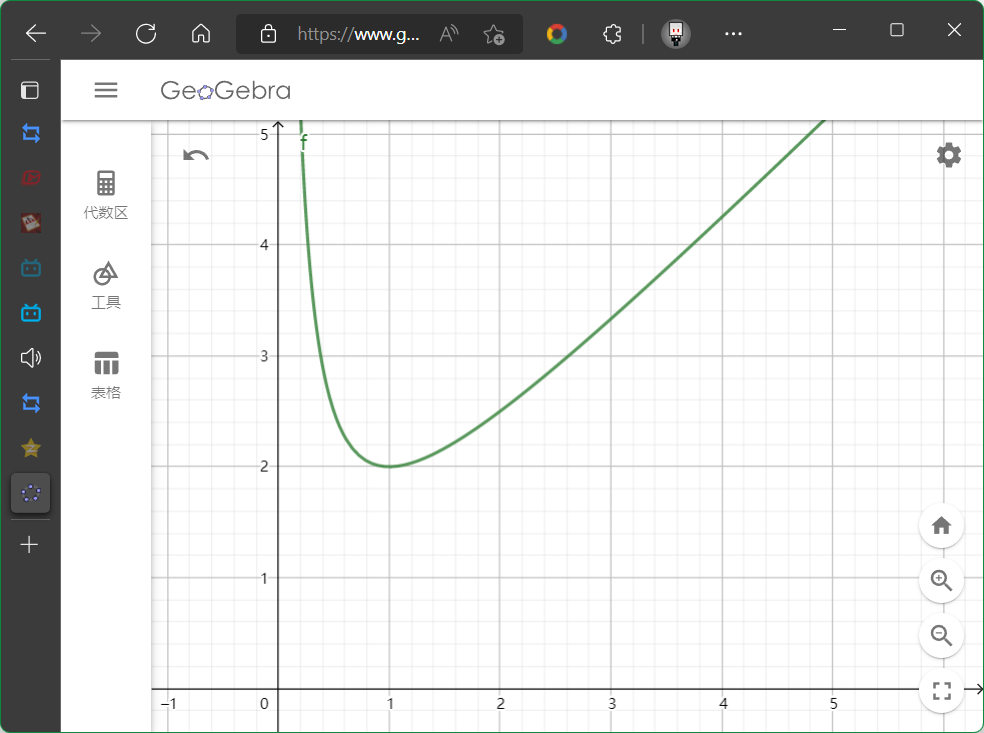
有渐近线(asymptote)的一个函数.

如何证明这件事? 留作练习Ex7.

东西有点多, 但是多学点知识总是好的.

函数的性质: 对称性(symmetry)

代数式表达

• 二次函数, 三次函数
• 镜子一样的等大的象, 小孔成像

定义(Def.)$f(x)$定义域为$D$, $\forall x\in D, -x\in D$, 如果$f(-x)=f(x)$, 称$f(x)$为偶函数.

定义(Def.)$f(x)$定义域为$D$, $\forall x\in D, -x\in D$, 如果$f(-x)=-f(x)$, 称$f(x)$为奇函数.

• 为什么? 一会解释.

也叫奇偶性.

学数学, 要有设身处地的直观感受!

像极了吞负号, 吐负号.

注意:

• (1) 全局性质
• (2) 定义域关于原点对称: $(-1,1), \mathbf Q, \R, \R^*, [-1,1)$是吗?
• (3) 分类: 奇, 偶, 非奇非偶, 又奇又偶($f(x)=0$).

为什么不叫轴心性? 最早发现的时候是去考察$x^n$的性质.

• (4) 如果$f(x)$是奇函数, $0\in D$, $f(0)=0$.
  • 如果如果$f(x)$是奇函数, $f(0)=0$?
  • 如果$f(x)$不是奇函数, $0\in D$, $f(0)\neq0$?
  • 如果$f(0)=0$, 则它不是偶函数?
  • 不能验证奇函数, 也不能用来验证是不是偶函数.
  • 如果如果$f(0)\neq 0$是奇函数, $f(x)$一定不是奇函数.
  • 用来排除奇函数, 或者求参数.

类似的现象, 你将在命题以及其关系一节学到.

总结: 学到了什么

切身体会, 带入自身学习数学

• 一些方法: 借助计算机, 树立学术诚信的高要求.
• 更重要的, 灵活运用这些方法.
• 祝大家玩的愉快!

知识相关

• 函数的性质
  • 单调性
  • 对称性的一部分(奇偶性).
• 几个特殊函数
  • 绝对值
  • 对勾函数

悬念

• 命题以及它们的关系.
  • 试着用你学过的"抽象"方法探索一下吧
• 还有上课没来得及讲解的练习题.
• 欢迎课下独立作答(不要一上来就敲电脑, 对自己要求高一点!)

End.

Good luck and have fun!

With great power comes great responsibility.