7EX

1. 计算: $$\frac{\left(2 x^{\frac{1}{4}} y^{-\frac{2}{3}}\right) \cdot\left(-3 x^{\frac{1}{4}} y^{\frac{1}{3}}\right)^{3}}{4 x y^{-\frac{2}{3}}}; $$ $$ 2 a^{\frac{1}{4}} b^{-\frac{1}{3}} \div\left(-\frac{1}{8} a^{-\frac{1}{4}} b^{-\frac{2}{3}}\right). $$

2. (1)若 $x>0$, 则 $\left(2 x^{\frac{1}{4}}+3^{\frac{3}{2}}\right)\left(2 x^{\frac{1}{4}}-3^{\frac{3}{2}}\right)-4 x^{-\frac{1}{2}}\left(x-x^{\frac{1}{2}}\right)=$ (2)化简: $$ (1+2^{-\frac{1}{32}})(1+2^{-\frac{1}{16}})(1+2^{-\frac{1}{8}})(1+2^{-\frac{1}{4}})(1+2^{-\frac{1}{2}}). $$

3. (1) 已知 $\sqrt{3 x-2}-\sqrt{(4-6 x)^{3}}=(x+y-1)^{2}$ , 则 $x^{\frac{1}{y}}$ 的值为 (2）若 $\sqrt[6]{4 a^{2}-4 a+1}=\sqrt[3]{1-2 a}$ , 则实数 $a$ 的取值范围是 $\mathrm{A}.\quad a \in \mathbf{R} \quad \mathrm{B}.\quad a=\frac{1}{2} \quad \mathrm{C} \quad a>\frac{1}{2} \quad \mathrm{D} \quad a \leqslant \frac{1}{2}$ (3) 若 $x^{-\frac{2}{3}}=2$ , 则 $x=$ .

4. 曲线$f,g,h,p$分别是$f(x)=a^x,g(x)=b^x,h(x)=c^x,p(x)=d^x$的图像, 判断$a,b,c,d,1$的大小关系.

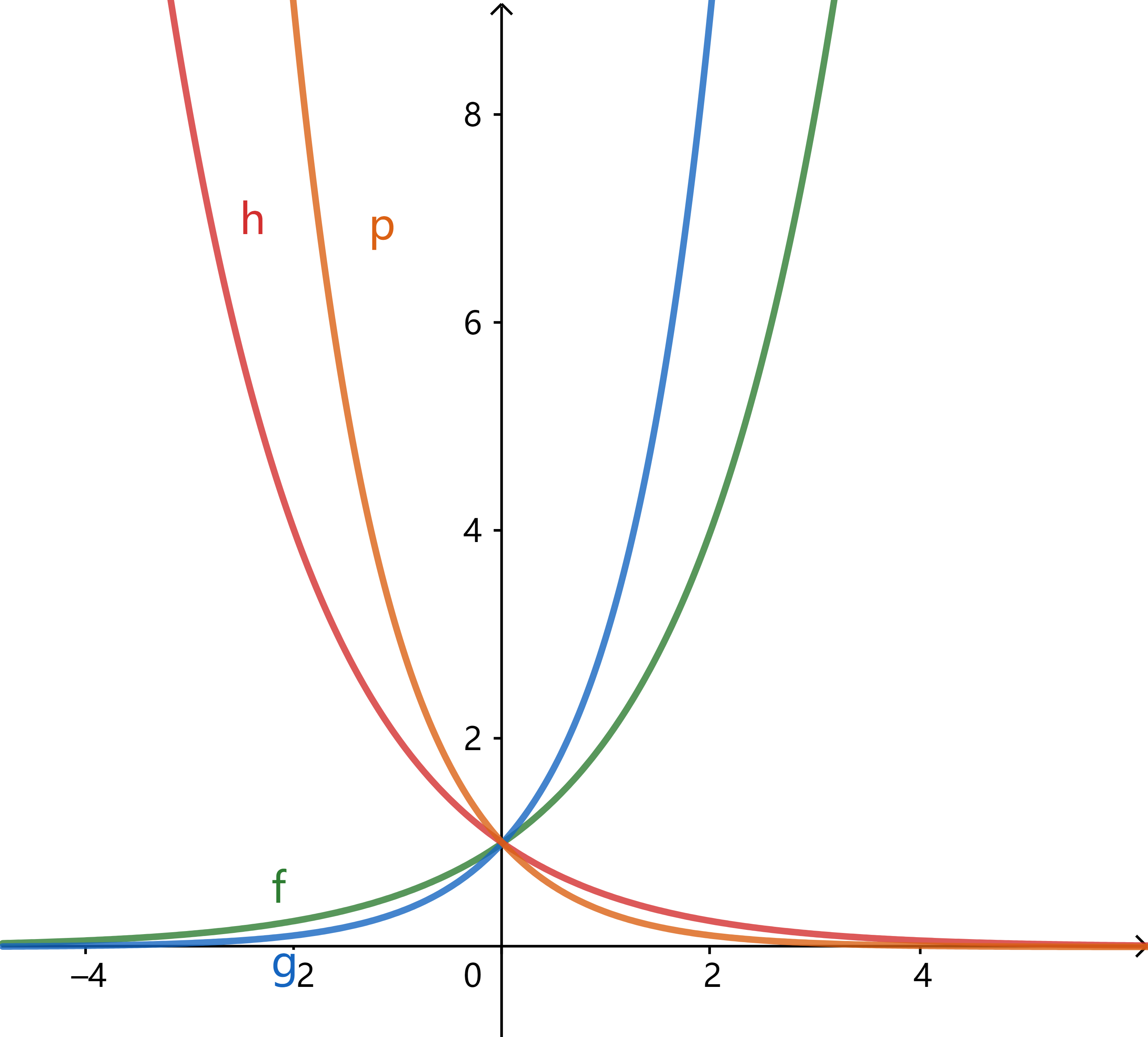
5. (1)若函数$f(x)=a^{3x-b}+1(a>0,a\neq1, b\in \R)$的图像恒过定点$(1,m)$, 求$b,m$的值. (2)在下图中, 二次函数$y=ax^2+bx$和指数函数$y=(b/a)^x$的图像只能是. 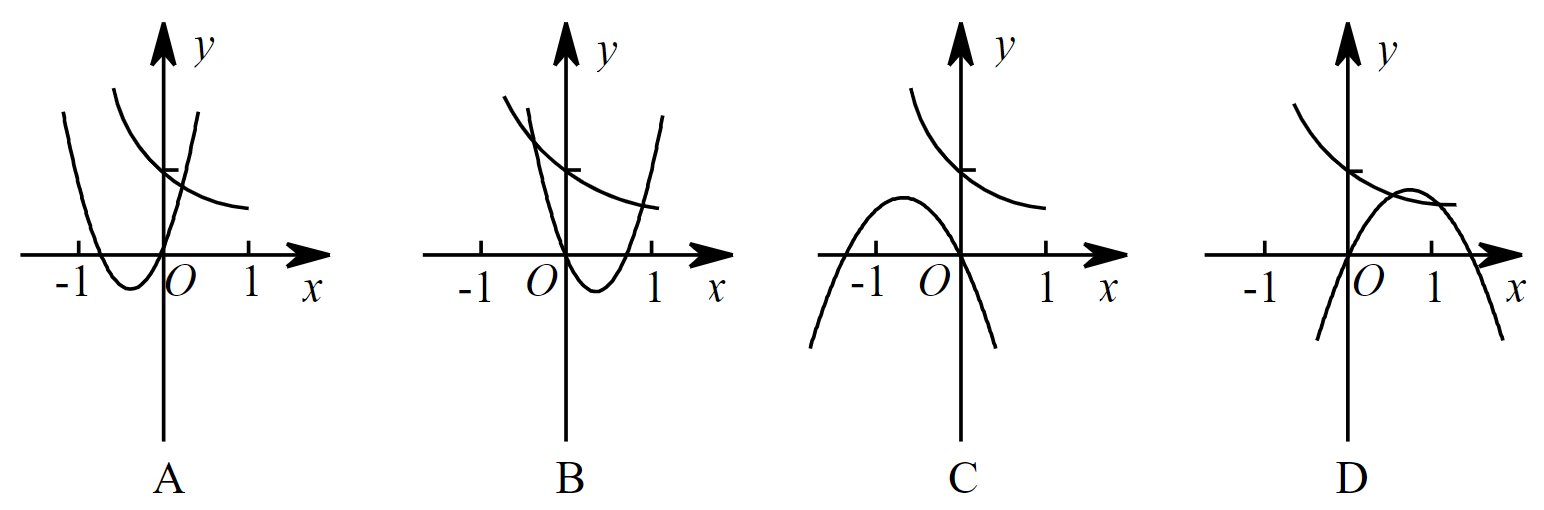(3)要得到函数 $y=2^{1-2 x}$ 的图象, 只要将函数 $y=\left(\frac{1}{4}\right)^{x}$ 的图象 ( ). A. 向左平移 $1$ 个单位 B. 向右平移 $1$ 个单位 C. 向左平移 $\frac{1}{2}$ 个单位 D. 向右平移 $\frac{1}{2}$ 个单位

6. (1)函数 $y=\left(\frac{1}{3}\right)^{x}(x \geqslant-1)$ 的值域为. (2)若函数 $f(x)=3^{x}+3^{-x}$ 与 $g(x)=3^{x}-3^{-x}$ 的定义域均为 $\mathbf{R}$ , 则（ ) . A. $f(x)$ 与 $g(x)$ 均为偶函数 B. $f(x)$ 为奇函数, $g(x)$ 为偶函数 C. $f(x)$ 与 $g(x)$ 均为奇函数 D. $f(x)$ 为偶函数. $g(x)$ 为奇函数

7. 用$\min{a,b,c}$表示$a,b,c$中的最小的数, 设$f(x)=\min{2^x, x+2, 10-x}(x\geq0)$, 求$f(x)$的最大值.

8. 若函数 $f(x)=\left{\begin{array}{l}(a-2) x, \quad x \geqslant 2 \\ \left(\frac{1}{2}\right)^{x}-1, x<2\end{array}\right.$ 是 $\mathbf{R}$ 上的单调减函数, 则实数 $a$ 的取值范围是（ ) . A. $(-\infty, 2)$ B. $\left(-\infty, \frac{13}{8}\right]$ C. $(0,2)$ D. $\left[\frac{13}{8}, 2\right)$