7LN - 指数函数(1)

指数函数contd

从逆运算的角度看指数函数

我们学过加法, 乘法, 它们都有逆运算. 指数也有, 我们后面回学习.

总之看下指数的定义: 有点难打, 大家应该都会, $n$个$a$相乘. 底数, 指数, 幂.

• 指数是正整数.
• 我们要拓展! $\N^*\to \N, a^0=1(a\neq 0)$.
  • 为什么? 要满足一些条件, 新定义要满足所有的运算法则.
  • 为了满足$a^ma^n=a^{mn}$.
  • 那么$a^n/a^n=1=a^0$, 而且分母不能为0.

$$ \left{\begin{array}{l} a^{m} \cdot a^{n}=a^{m+n} \\ a^{m} / a^{n}=a^{m-n} \\ \left(a^{m}\right)^{n}=a^{m \cdot n} \\ (a b)^{n}=a^{n} b^{n} \end{array}\right. $$

• 我们还要拓展! $\N \to \Z$怎么办?
  • $a^{-n}=1/a^n$.
  • 问: $(1/3)^{-4}$.
• 我们还要拓展! $\Z \to \textbf{Q}$怎么办?
  • $a^{1/n}$怎么说?
  • 我们知道$(a^{m/n})^n=a^m$, 那就挺好的. 那就是表示$\sqrt[n]{a^m}$.
  • 哦, 那你就明白了, 所有的规则都是一样的.
  • (1)另一种视角: $a^{m/n}=\sqrt[n]{a^m}=(\sqrt[n]a)^m$
  • 这两个式子一样吗? 用$a^{4/6}$举一个例子.
    • 令$a=-1$, $a^{4/6} \quad ?\quad a^{2/3}$, 一样吗?
    • 不行, 要求$m,n$既约(已经约分干净了, 也就是互质).
    • 其余的都可以吗? $a^{1/2}$
    • 能算的都能算, 不能算的两个都不能算. 这才叫保持一致(consistency).
  • (2)负分数指数: $a^{-m/n}=1/a^{m/n}$.
• 一点预告:
  • $a=-1$真的不能算吗? 后面我们会学$i=\sqrt{-1}, 以及\textbf{C}$.

例子: 计算$(16/9)^{-3/2}$. ($27/64$).

好耶! 我们已经拓展到了有理数了!

• $\textbf{Q} \to \R$ 不会!
  • 为什么? 因为我们不知道什么是无理数.
  • 我知道啊, 无限不循环小数啊!
  • 知道=知道一定可以怎样生成.
  • 由于加减乘除运算的封闭性, 暂时还得不到这样的结论.
  • 开根号不可以吗?
  • 这是无理数的一小部分(代数数, 某一个多项式的根)
  • 其他部分叫做超越数. $\pi, e$等等, 我们不知道如何得到的.
  • 可以无限去逼近. 想要多接近, 就有多接近.
  • 这个过程通常被成为"夹逼".
  • (1)是实数
  • (2)满足前面的所有运算法则

看点例题

• Ex.1

  • 技巧: 答案一定形如 $?x^?y^?$.
  • 认识式子结构, 关注每一个部分, 会快很多.
  • 练习口算, 既快有准.
  • $-27/2x^0y^1$.
  • 推荐时间, $<10\text{s}$

• Ex.2

  • (1)$4x^{1/2}-3^3-4x^{1/2}+4$.
  • (2) 请大家化简.
    • 不是把所有括号打开=化简!
  • 不要写成"开多少次方分之一"的情况
  • 不过也很正常, 大家新学一个东西, 都有这样的想法

我■, 又■■要学一个新东西, 老子不要!

• 观察式子有什么关系. 注意$(n+m), (n^2+m^2), (n^4+m^4)\cdots$

• 就像以前一样, 观察它们之间的关系而不是形式.

• 关系是平方. 派一个$(n-m)$就行了! Easy!

• 答案是$(1-1/2)/(1-2^{-1/32})=1/2(1-2^{-1/32})^{-1}$. 尽量用分数指数来写, 会方便很多.

• Ex.3 (5min)

  • (1) 看定义域. $8/27$.
  • (2) 注意绝对值. D. (初中知识)
  • (3) $\pm {\sqrt2\over4}$.
    • 最终要分母有理化.

为什么我们要这么干?

• 什么数都能算, 这个过程, 形成了函数!
• 有什么关系

指数函数

一些定义

• (1) $f(x)=a^x, a>0, a\neq1$.
  • 这个定义的原因, 比如$-1$作为底数, 有的能算, 有的不能算, 很烦人. 高中不研究, 而且$(-1)^{\pi}$咋整?
  • $a=1$太没劲. 研究的时候形式不太一样.
  • 只有长成这样的叫指数函数. 其他的都不叫.

判断: $2^x, 2^x+1, (1/2)^x, 2^{-x}.$

图像与性质

• 描点, 画图. 请画出$y=2^x, y=(1/2)^x$.
• 一二象限最好多一点. 因为它们都是正数.

这是两个代表, 下面看一些性质. (1) 定义域$\R$, 值域$(0,+\infty)$, 渐近线为$y=0$. (2) 单调性: $a>1$, 在$\R$上增. $a$大就增, 小就减. (3) 对称性: 没有. (4) 定点: $(0,1)$.

• 可以有$(0,1),(1,a)$.

• 注意大小关系.

• Ex4. 我要画$x=...$

特性(性质)

• (1) $y=a^x$与$y=(1/a)^x$关于$y$对称.
• (2) 当底数大于1的时候, 增长非常快. 快到一切我们能想到的其他函数. $x^2 \text{ v.s. } 2^x$.
  • 关于国际象棋和$2^{64}$的一个故事.
  • 等于

Fun idea: 如果围棋发明者问你呢?

一张纸$0.1\text{mm}$, 42次就可以从地球到月球.

看$y=1.1^x$的图像的样子.

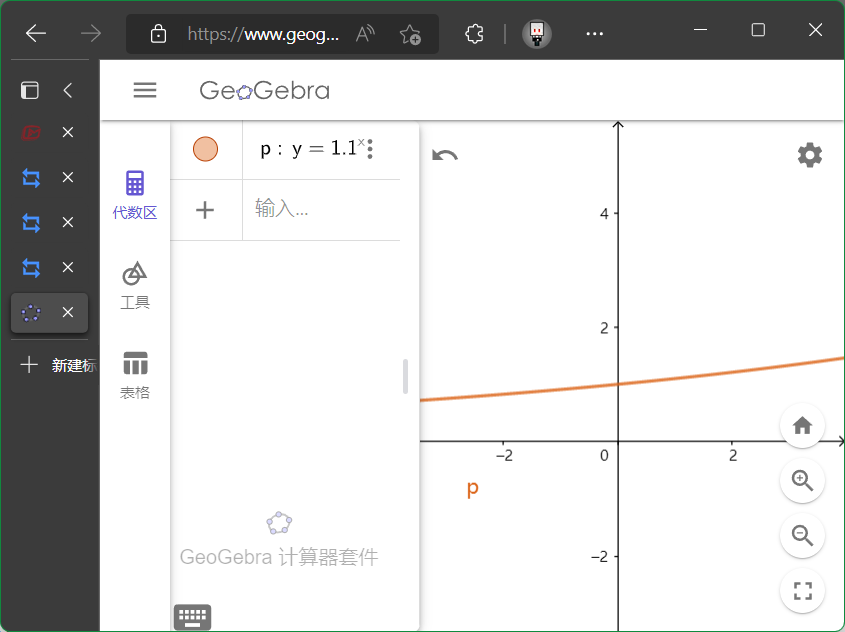
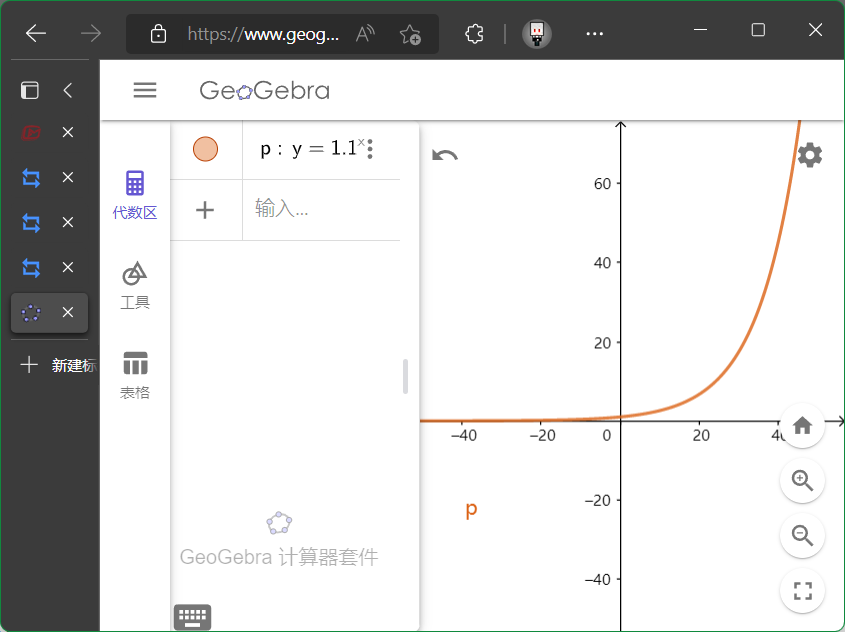
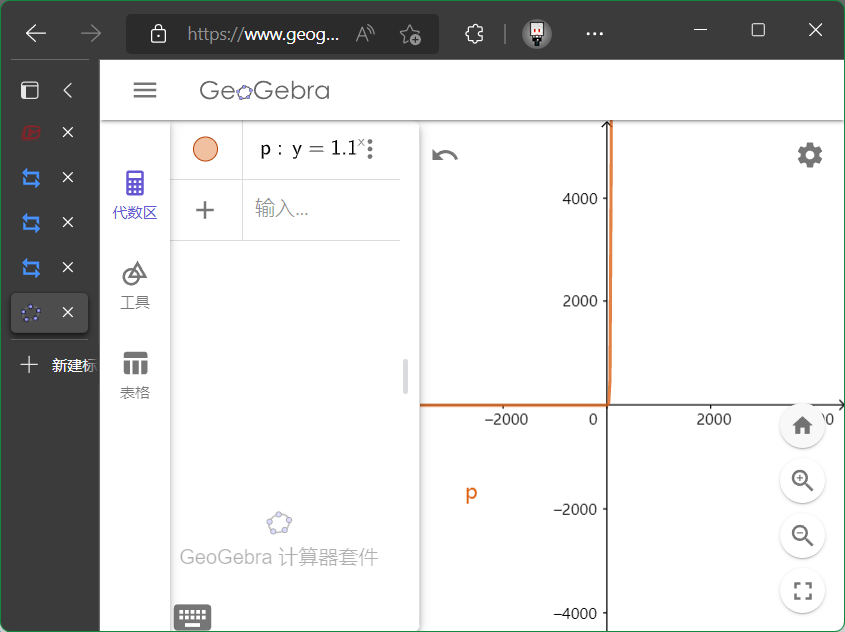
这就解释了一个鸡汤$(1.01)^{365}\approx37.8$. 这就解释了一个鸡汤$(0.09)^{365}\approx0.09$.

其实本质原因是学习缺乏一个量化的及时反馈. 很难量化! 而且在短期内可能看不见成效. 但不要放弃, 你可以认为努力总有回报.
但是一天提高1%终究还是很困难的, 因为积累量大的情况下就很难完成.
请大家每天提升一点点吧!

看例题

• Ex. 5
  • (2) 我们知道$0\le b/a\le 1$, 但是分不清正负, 但可以判定对称轴. ($\alpha$)
  • 有没有可能还有谁? 画出所有的满足的
  • 还可以开口向下的!
  • (3) 左加右减. $((1/4)^{-1/2})^{1-2x}$
• Ex. 6
  • 用定义!
  • 有单调性, 自变量最小函数值最大.

练习: $3^x, x\in[-2,3]; \qquad 1/2^x, x\in[-3,6]$.

• 出题人是怎么想的?

• Ex. 7(作业6)

你可能好奇, 刚刚的东西是什么?

用Python库计算?

• 下载Python
• 执行pip install ipython
  • pip是包的安装器, 这个包就是许多开发人员开发的一些文件. install是安装的意思, ipython是一个对新手很友好的工具.
• 经过漫长的等待之后, 输入ipython.
  • 其实不用那么漫长, 需要换镜像源, 看我们演示.
• 加减乘除都没问题.
• 我这里比较好看是因为用了Windows Terminal, 字体比较统一.

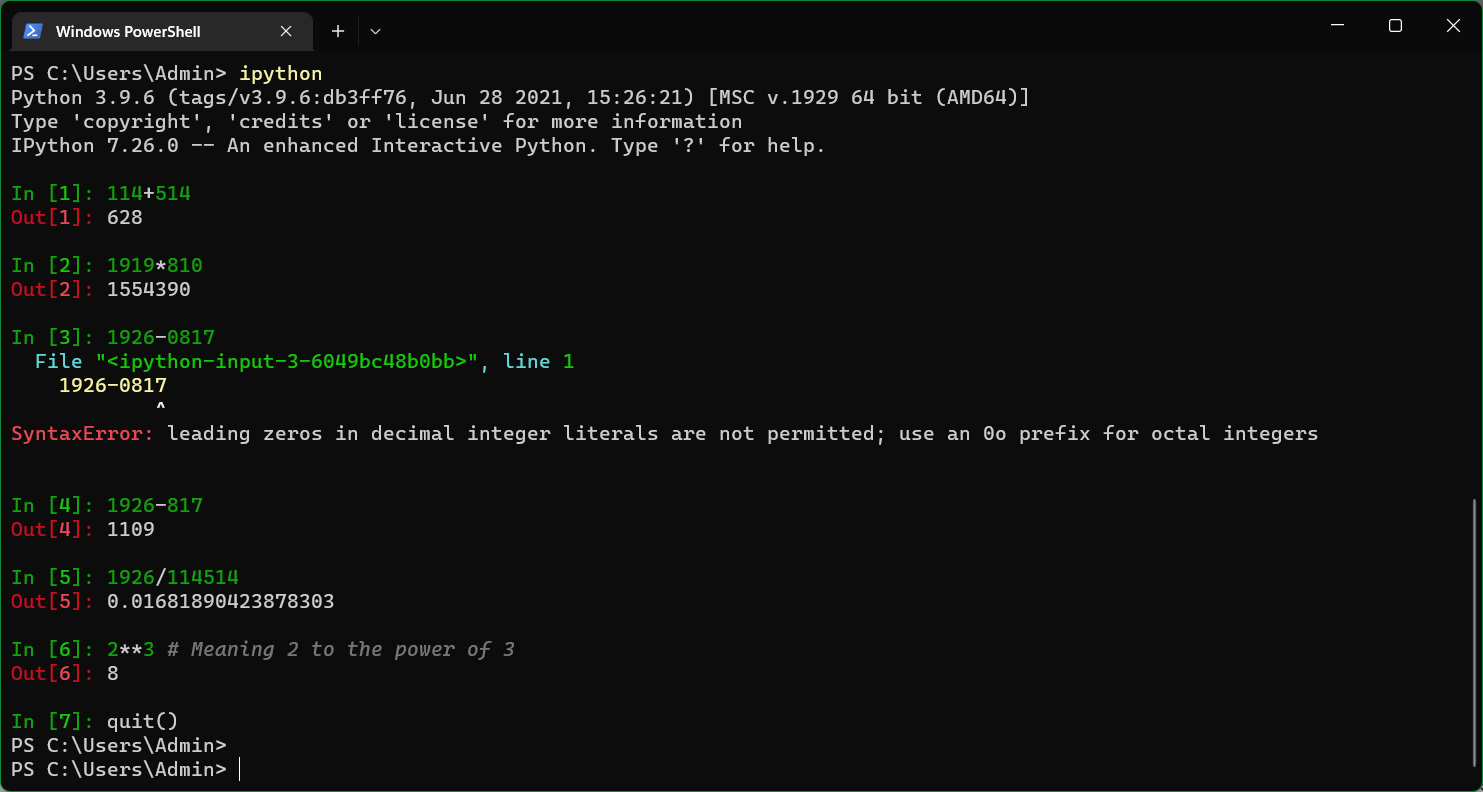
• in是我输入的, out是python的输出,
• 第三行的输入错了, 看到它会报错(Syntax Error, 语法错误), 翻译过来就是十进制整数文字中的前导零是不允许的；对八进制整数使用 0o 前缀.
• 这些信息就当阅读理解做就行了, 不难, 不会的词就上网查, 也很方便.
• 这就解释了为什么我每次讲义都有英语的对应标注(方便进一步探索).

总结: 学到了什么

其实你应该发现了, 正经的知识点前面都有括号标示序号. 比如(1)(2)这样的.

你还注意到了如何用python进行表达式求值.

你也可以学习下一些常见的概念, 这些都不简单, 但是如果你掌握了这些技巧并且加以应用的话, 那么未来很多难题的解决不过是花点时间写一个程序而已!

End.

May the force be with you.

为什么接触英语?

随着科学技术的发展, 在国际学术交流中使用英语已经成为常态: 顶尖的论文无一不使用英文来书写, 在国际上公认的计算机领域经典书籍也是使用英文编著. 顶尖的论文没有中文翻译版; 如果需要获取信息, 也应该主动去阅读英文材料, 而不是等翻译版出版. "我是中国人, 我只看中文"这类观点已经不符合时代发展的潮流, 要站在时代的最前沿, 阅读英文材料的能力是不可或缺的. 阅读英文材料, 无非就是"不会的单词查字典, 不懂的句子反复读". 如今网上有各种词霸可解燃眉之急, 但英文阅读能力的提高贵在坚持. "刚开始觉得阅读英文效率低", 是所有中国人都无法避免的经历. 如果你发现身边的大神可以很轻松地阅读英文材料, 那是因为他们早就克服了这些困难. 引用陈道蓄老师的话: 坚持一年, 你就会发现有不同; 坚持两年, 你就会发现大有不同.