8LN - 指数函数和简单的对数运算(2)

开始之前

相信大家经过昨天的鸡汤, 已经信心满满, 准备学习.

比较大小

举个例: $0.8^{-0.5}~~?~~~0.8^{-0.6}$

• (1) 同底不同指
  • 考察指数函数的单调性,
  • 比如$0.8^x$.
• (2) 同指不同底
  • 画两个函数图像去比较? (找$x=1$的时候!).
• (3) 不同底不同指
  • 找中间量(1).

例子: $2.5^{0.1}0.9^{3.4}$ $3^3\pi^\pi$.

• 考虑$3^\pi$, 和一边同底, 和另一边同指.
• 选$\pi^3$可以吗? 可以的!
• 画成图, 就是:

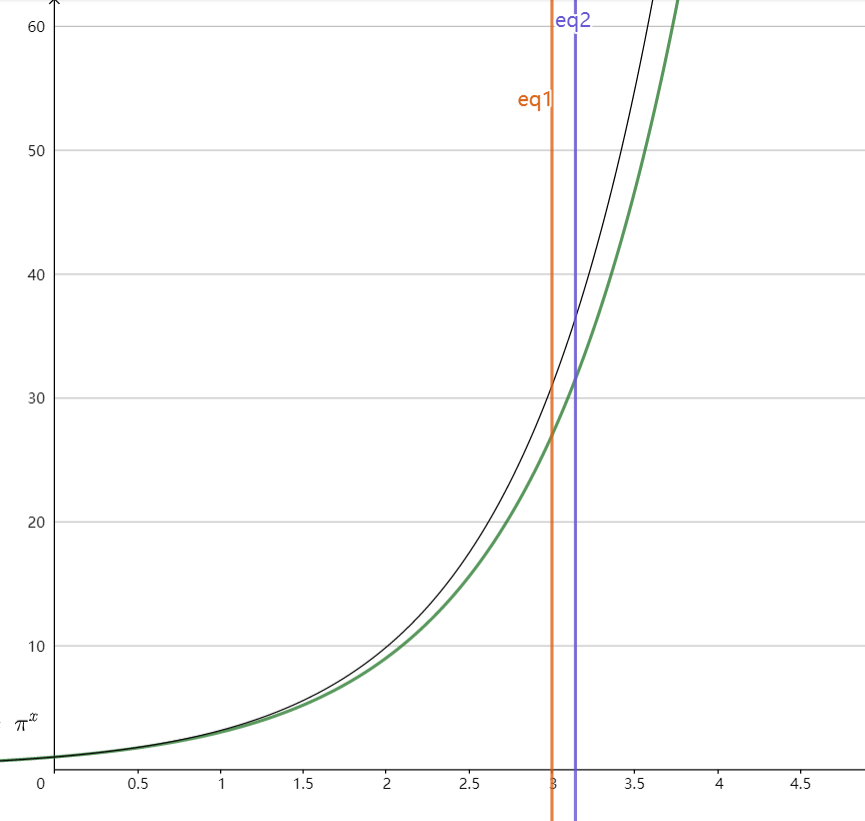
那么问$3^\pi ~~~~ \pi ^3$?

想先找几个试试看: $$ 3^4>4^3\\ 2^3<3^2 $$

有点迷惑. 我们不管了.

其实还有一些和上面一样的, $0.6^{0.6}~~~~0.7^{0.7}$, 用计算机试试看.

• 看Ex.1(1)(2)

指数函数和其他函数的复合

像往常一样, 求定义域, 值域, 单调性, 对称性等等内容.

• $0^0$无意义
• 一层一层求就行了
  • Ex.2(2)
• 经过一些复合可以有对称性.
  • Ex.2(1)

关于特殊值:

• 一定要用特殊值?

• 一定不能用特殊值?

  • 考试: 怎么快怎么搞
  • 下来: 传统的方法要会.

• 特殊值可以解决一切问题, 认识清楚就可以用.

• 其实0比1还省事. 就是看看有没有定义.

• 对称性(contd)

  • Ex2.(5)

代进去几个试试看, 哦? 也就是$f(1/2+x)+f(1/2-x)=1$. 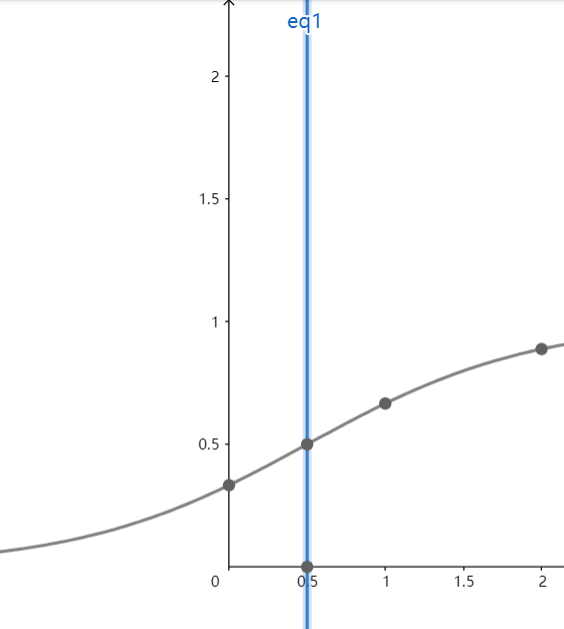能推倒吗? 留个悬念.

• 看Ex.3:
• 想想会出成什么样? 它们都表示二次函数.

说到16A.D.的欧洲

• 天文学蓬勃发展, 计算成为了主要的障碍. (数据非常不友好)
• Scotland的Napir说乘法有简单的方法.

$$ \begin{aligned} &1 &2~~~ &3 &4 ~~~~ &5 &6 ~~~~ &7 \\ &2 &4 ~~~ &8 &16~~~~ &32 &64 ~~~~&128 \end{aligned} $$

• "列竖式, 慢就在这了."
• "可以把乘法换成加法."

但是Napir的表格是按照第二行排列的. 也就是:

$$ \begin{aligned} &1 &\color{red}? \color{black} ~~ &2~~~ &3 &4 ~~~~ &5 &6 ~~~~ &7 \\ &2 &3 &4 ~~~ &8 &16~~ &32 &64 ~~~~&128 \end{aligned} $$

3应该也可以写成这样. 大概是$1.x$.

当然, 他花了20年出版了一本书, 里面就两行数, 很多页. 销量第一.

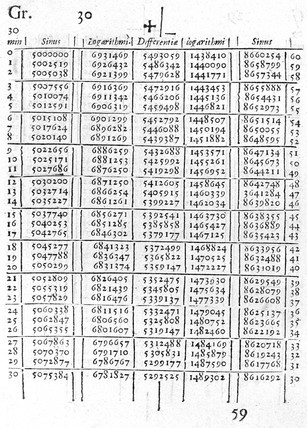
所以我们就想知道$2^?=3$.

这个工具的诞生使得天文学家的寿命加倍.

我们更关注它的"性质"而不是"结果", 因此我们可以用一个符号来代表它.

"我们给他起一个$\log_23$". 可以不用写 $\cancel{\log_2^3}$. 我们起名字叫做对数.

对数

为什么叫对数?

• 表"对着"的那个东西才能算. $m=\log_ab$

一些约定: $$ \Huge m=\log_ab\qquad a^m=b $$ 意思是: $a$的多少次方等于$b$? 那个答案就是$m$.

• $a$在底下, 右边$a$也在底下. $a>0, a\neq 1$.
• $b$是真数, 就是那个结果, 真数大于0.
• $m$叫做对数
• 它们可以互换, 我们可以在不清楚的时候想想.

例如: $\log_28=?;\log_{1/3}9=?;\log_{27}9=?;\log_{16}8=?$

奇怪的银行

有一个奇怪的银行, 它每年的利息是100%. 所以第一年你存了100, 第二年, 你就得到了200元. 能不能这样, 在年中的时候取出来, 然后再存进去, 好像本金就多了, 回报也多了. $100\rightarrow150\rightarrow225$ 哦, 看上去很好的, 为什么只取一次呢? 一直取, 一直存, 一直取, 一直存...

那么这么干, 100元能变成什么? 真正的收益是... 大约272元.

$(1+1)^2=2$ $(1+1/2)^2=2.25$ $(1+1/3)^3\approx2.37$ $(1+1/4)^3\approx2.44$ ... $(1+1/10)^10\approx2.59$ $(1+1/100)^100\approx2.70$ 这样的函数是$(1+1/x)^x$, 增函数, 但是这个数有上限, 一定小于3.

我们认为它有渐近线!

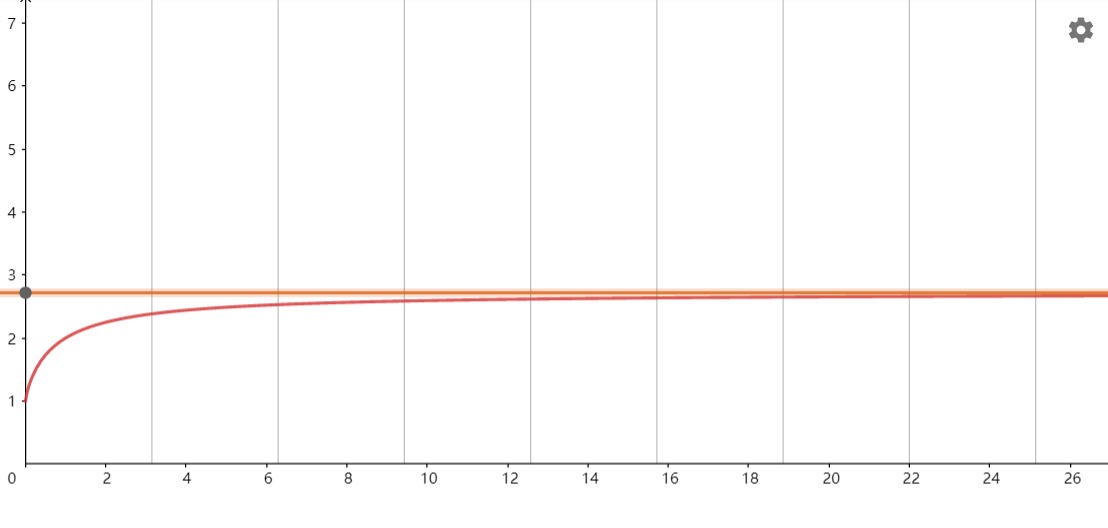
这个渐近线的$y$值是几呢? 最早的研究者Euler证明了它是一个超越数. 因此命名叫做叫$e= \textbf{2.7}1828459045235360\cdots$.

和对数的关系

• (1)自然对数: 我们可以以$e$为底数, 就用$\log_eM=\ln M$.
  • 为什么用它? 在导数一节会解释.(留个悬念)
• (2)常用对数: 以10为底数, 就得到了$\log_{10}M=\lg M$.

其实我觉得应该换一下两个的名字.

性质与运算法则

(1) 对(废)数(话)恒等式: $$ a^{\log_ab}=b. $$ 一句废话.

这有什么意思? 任何数可以写成任何为底的指数. (用得着的)

比如$8=2^3=3^{\log_28}$

(2) 关于1: $$ \log_a1=0,\log_aa=1 (a>0, a\neq1). $$

(3) 运算 (注意, $\log$的优先级高于乘法, 注意括号!) $$ \begin{aligned} \log_aM+\log_aN&= \log_aMN \\ \log_aM-\log_aN&= \log_a(M/N)\\ \log_a(M^\alpha)&= \alpha\log_aM(真数有指数, 可以往前拽)\\ \end{aligned} $$ 看例子:

• 看Ex4.(1)(2)(3.1)
• (3.2)有点困难, 算$a$不出来. 就带着对数做就行了.
• (4)

但是只能做底数相同的对数. 以2为底和以3为底真的一点没有关系吗?

(4) 换底公式

$$ \log_aM \sim \log_bM $$ 改成指数式, $a^x=M, b^y=M, a^x=M=b^y$.

$b^{\log_b(a^x)}=b^{x\log_b(a)}=b^x$, 那么$y=x\log_b a$. 哦, 我们就有了$\log_bM=\log_aM\log_bM$. 有点麻烦, 所以我们变形: $$ \boxed{\log_aM={\log_bM\over\log_ba}} $$

快刀切对数. 举几例子.

几个小公式:

• $\log_ab\cdot\log_ba=1$.
• $\log_{a^m}b^n={n\over m} \log_ab$.

上面的还在上面, 下面的还在下面.

• 看Ex4.(5)(-12)
• (6)(7).
  • 观察代数结构的提炼.

总结: 学到了什么

感到难?

太正常了! 我校的一位NOI银牌的同学说:"当时学的时候太难了, 感觉非常震惊."

总结

• 对数的指数式子
• 对数的运算
• $\color{red}请一定要熟练!$
• 对数的那些公式在两个对数乘的时候不太好用.
• 自己慢慢体会, 有任何问题(1) 回归指数式 (2) 快去问!

作业

Ex(5)(6).

悬念

什么是$e$? 推荐微积分的本质!!!

比较通俗易懂, 很好玩.

End.

Raise the bar!

番外篇: 数学素养(mathematical maturity)的定义

(节选)