9LN
-
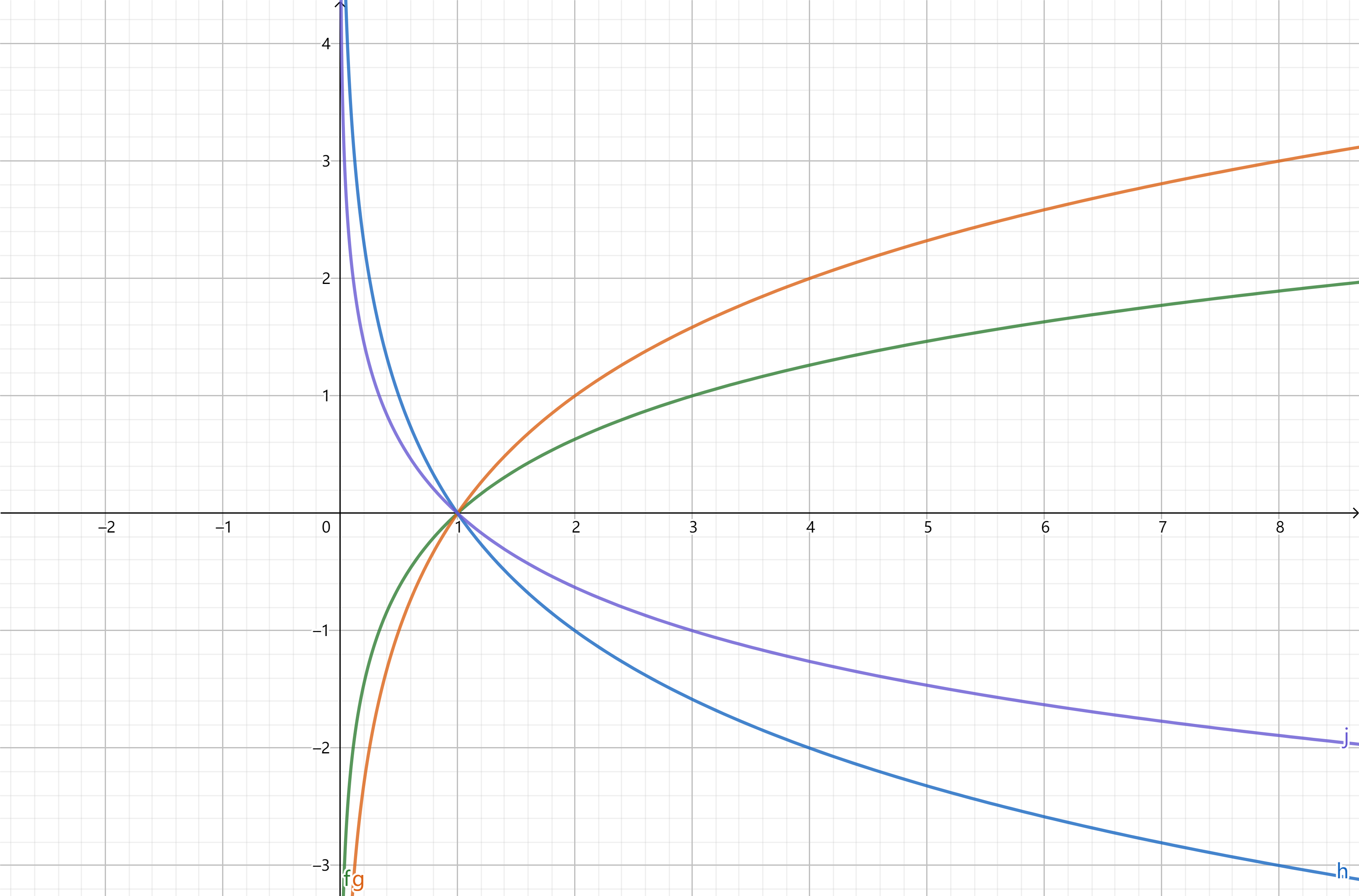
曲线$f,g,h,j$分别是$f(x)=\log_ax,g(x)=\log_bx,h(x)=\log_cx,j(x)=\log_dx$的图像, 判断$a,b,c,d,1$的大小关系.
-
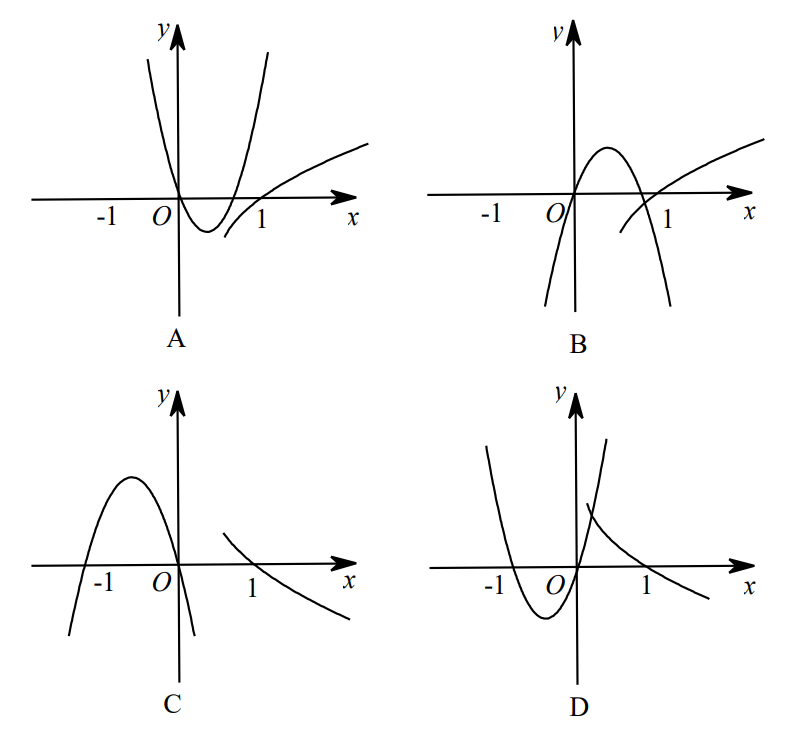
函数 $y=a x^{2}+b x$ 与 $y=\log _{\mid \frac{b}{a}} x \quad(a b \neq 0,|a| \neq|b|)$ 在同一直角坐标系中的图象可能是:
-
比较大小: $\log_{0.3}5~~~~\log_0.36$; $\log_{0.3}6~~~~\log_{0.2}6$; $\log_{3}{1\over5}
\log_{1/2}2/3$; $\log_{1\over3}{1\over4} -
(1)设$a=\log _{3} \pi, b=\log _{2} \sqrt{3}, c=\log _{3} \sqrt{2}$ , 则() A. $a>b>c$ B. $a>c>b$ C. $b>a>c$ D. $b>c>a$ (2) 函数 $f(x)=\left{\begin{array}{l}\log _{2} x, x>0 \\ \log _{\frac{1}{2}}(-x), x<0\end{array}\right.$ , 若 $f(a)>f(-a)$ , 则实数 $a$ 的取值范围是( ) A. $(-1,0) \cup(0,1)$ B. $(-\infty,-1) \cup(1,+\infty)$ C. $(-1,0) \cup(1,+\infty)$ D. $(-\infty,-1) \cup(0,1)$ (3)设 $a>0, a \neq 1$ , 函数 $f(x)=\log _{a}\left|\frac{1-x}{1+x}\right|$ 在 $(1,+\infty)$ 上单调递减, 则 f(x) 满足( ) A. 在 $(-\infty,-1)$ 上单调递减, 在 $(-1,1)$ 上单调递增 B. 在 $(-\infty,-1)$ 上单调递减, 在 $(-1,1)$ 上单调递减 C. 在 $(-\infty,-1)$ 上单调递增, 在 $(-1,1)$ 上单调递增 D. 在 $(-\infty,-1)$ 上单调递减, 在 $(-1,1)$ 上单调递减
-
(1) 若 $f(x)=\frac{1}{\sqrt{\log _{\frac{1}{2}}(2 x+1)}}$ , 求 $f(x)$ 定义域, 值域, 单调性. (2.1) 已知 $x \in[1,8]$ , 求函数 $g(x)=\left(\log _{2} \frac{x}{2}\right)\left(\log _{2} \frac{x}{4}\right)$ 的值域. (2.2) $f(x)=2+\log_3x(x\in[1,9])$, 求$y=[f(x)]^2+f(x^2)$的值域. (3) (2010 湖北文数) 已知函数 $f(x)=\left{\begin{array}{l}\log _{3} x, x>0 \\ 2^{x}, x \leqslant 0\end{array}\right.$ , 则 $f\left(f\left(\frac{1}{9}\right)\right)=$ A. $4$ B. $\frac{1}{4}$ C. $-4$ D. $-\frac{1}{4}$
-
求下列函数的反函数: (1) $f(x)=3x+2$; (2) $f(x)=3\times 2^{x+1}$; (3) $f(x)=x^2+1$, $x\in [-3,0]$; (4) $y=\dfrac{6x+5}{x-1}, x\in\R, x\notin1$.
-
给定实数 $a(a \neq 0,1)$ , 设函数 $y=\frac{x-1}{a x-1}\left(x \in \mathbf{R}\right.$ 且 $\left.x \neq \frac{1}{a}\right)$ , 证明该函数图象关于直线 $y=x$ 对称. 你还能想到哪些函数自己是自己的反函数?
-
$f(x)=\sqrt[3]{x+\sqrt{1+x^{2}}}+\sqrt[3]{x-\sqrt{1+x^{2}}}(x \in \mathbf{R})$的反函数是.
-
(1) 设 $a=\log _{5} 4, b=\left(\log _{5} 3\right)^{2}, c=\log _{4} 5$ , 则( ) A. $a<c<b$ B. $b<c<a$ C. $a<b<c$ D. $b<a<c$ (2) 设 $f(x)=\left{\begin{array}{l}\mathrm{e}^{x}, x \leqslant 1 \\ f(x-1), x>1\end{array}\right. , 则 f(\ln 3)=(\quad)$ A. $\frac{3}{e}$ B. $\ln 3-1$ C. $e$ D. $3 \mathrm{e}$
-
(1) 从奇偶性看:函数 $y=\ln \left(x+\sqrt{x^{2}+1}\right)$ 是 (2)设函数 $f(x)$ 是定义在 $\mathbf{R}$ 上的奇函数, 若当 $x \in(0,+\infty)$ 时, $f(x)=\lg x$ , 则满足 $f(x)>0$ 的 $x$ 的取值范围是 (3) 若 $a>1$ , $b>1$ 且 $\lg (a+b)=\lg a+\lg b$ , 则 $\lg (a-1)+\lg (b-1)=$. A. $\lg 2$ B. $1$ C. 不是与 $a$ , $b$ 无关的常数 D. $0$