9LN - 对数函数, 幂函数

前情提要

我们讲到了一个对数的东西. 我们先回顾下.

$\log_ab$ 上节课, 我们的"换底公式"证明方法和课本很是不一样, 请阅读课本上的证明过程, 想一想, 为什么课本会这样证明?

能不能给他找一个理由?

对数相加, 真数相乘; 对数相减, 真数相除; 真数有指数, 可以往前拽.

例子: $4^{\log_23}$

对数函数

既然我们可以往对数里面塞各种各样的正实数, 那为什么不用函数来表示呢?

(1) 对数函数: $y=\log_ax(a\neq 1, a>0)$.
- 对它进行改造的都不行!
(2) 定义域:$(0,+\infty)$. 真数必须大于0. !

图像

注意, 二三象限没有图像, 可以空间稍微压缩一点. 来画: $y=\log_2x, y=\log_{\frac{1}{2}}x$的图像.

(3) 值域: 有没有上界? 但是依然可以涨到无穷.
(4) 单调性: 增/减.
(5) 对称性x
(6) 定点$(1,0)$.
(7) 重要的点: $(a,1)$.

指数函数和对数函数都满足大(于1)增, 小(于1)减.

看Ex1.

一些特性

(1) $y=\log_ax$与$y=\log_{1\over a}x$关于$x$轴对称.
(2) 对数函数是非常慢的函数.
- 增长快的可以很好的降下来.
- 比如地震的级别, 声音的计量.

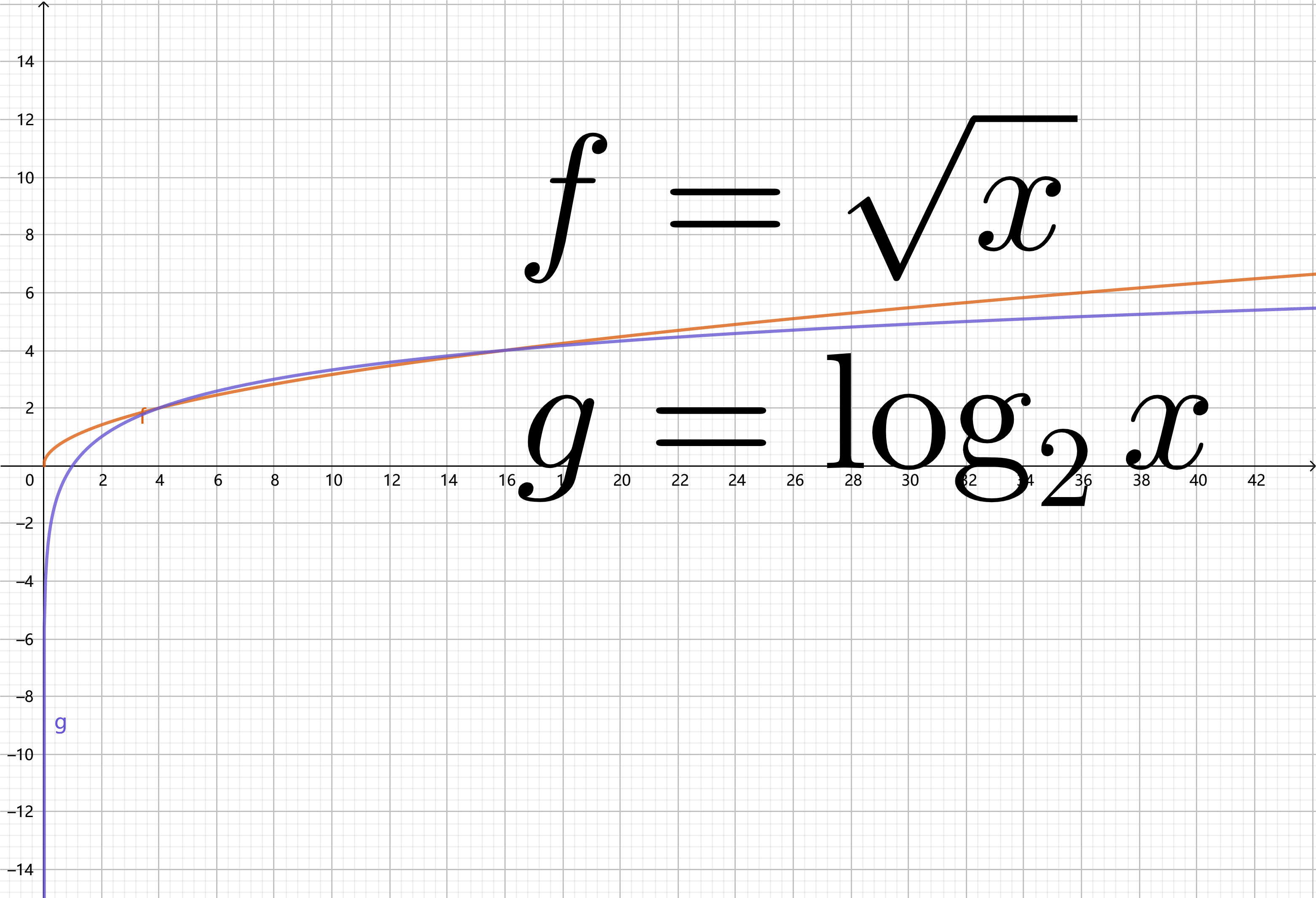
震级的定义: 震动的幅度/基准震动...

可是这东西一除出来就太大了!
"在xx发生了11451419.19级的地震" 所以就取10的对数, 好降下来. 但是这是在对数层面的, 也就是说越往上走越极端! 增长快的取对数就可以降下来.
(3) 对数函数和指数函数挺像: 把$x,y$颠倒一下.
- 关于$y=x$对称.
- 为什么? $(m,n)\rightarrow (n,m)$.
看Ex.2.
- 1. 满足$0<|b/a|<1$
- 1. 满足$|b/a|>1$

Ex3(1)(2)(3), 4(1).比较大小:

同指不同真: 构造函数的单调性
不同底同真: 两个图像
不同底不同真: 中间量(0,1).

学的东西越多, 改的东西也越多.

小技巧: $(0,1),(1,+\infty)$, 同一区间正, 不同区间负.

对数函数和其他函数的复合

注意定义域!

抵消掉的"函数"

还有很多函数关于$y=x$对称!

$f$干啥, $g$就弄回来.
这样叫做"反函数", 核心是把自变量当函数值, 把函数值当自变量.
原函数$f(x)$, 反函数$f^{-1}(x)$($f$逆$x$)
经常称作两个函数互为反函数.

什么样的两个函数具有满足$y=x$对称的潜力?

双射!
Ex6. $x,y$对调, 解个方程就行了...

性质:

关于$y=x$对称;
定义域, 值域互换.

Ex.7

所以以后求值域, 有时候可以求反函数的定义域. $y=ka/x$...

Ex.8

这货好难啊!
先换元, 再三次方.

$$ \begin{array}{l} y=f(x)=\sqrt[3]{x+\sqrt{1+x^{2}}}+\sqrt[3]{x-\sqrt{1+x^{2}}} .\\f{(x)}=\sqrt[3]{a+b}+\sqrt[3]{a-b}\\ y^{3}=2 a +{3(a+b)^{\frac{2}{3}}(a+b)^{\frac{1}{3}}} +{3(a+b)^{\frac{1}{3}}(a-b)^{\frac{2}{3}}}\\=2a+ \underbrace{3(a+b)^{\frac{1}{3}}(a-b)^{\frac{1}{3}}}{-3}[\underbrace{\left[(a+b)^{\frac{1}{3}}+(a-b)^{1\over3}\right]}{y}] \end{array} $$

与往常的分离变量直接的方法不同, 这个是整体构造.
就像以前的$x+1/x=3,$问$x^2+1/x^2$的结果.

幂函数

幂就是几次方, 也可以叫做函数. $y=x^2$. ~~底数函数~~ $y=x^a$.

初中函数里面就学了这个, 学了三年.
以后会有更多的知识.
它们都是好函数(光滑, 连续, 有很多性质, 还有函数图像)
后面还有更多形如Dichlet函数一样的函数.
- Stay tuned.
越学越无知.

请画出: $y=x^1,y=x^2,y=x^3,y=x^{1/2},y=x^{-1},y=x^0$.

如此千奇百怪的函数还能叫做幂函数?

总结: 学到的什么

对数函数, 和对数函数的复合.
反函数
幂函数, 开了一点小头.